SPSS enkel linjär Regression Tutorial

SPSS enkel linjär Regression Tutorial

1. skapa Scatterplot med anpassad linje
2. SPSS linjära Regressionsdialoger
3. tolka SPSS Regression Output
4. utvärdera Regressionsantagandena
5. APA riktlinjer för rapportering Regression

forskningsfråga och data

Företag X hade 10 anställda ta ett IQ och jobbprestanda Test. De resulterande data-varav en del visas nedan – är i enkel linjär regression.sav.

det viktigaste företaget X vill räkna ut ärförutsäger IQ jobbprestanda? Och – i så fall-hur?Vi svarar på dessa frågor genom att köra en enkel linjär regressionsanalys i SPSS.

skapa Scatterplot med anpassad linje

en bra utgångspunkt för vår analys är en scatterplot. Detta kommer att berätta om IQ och prestationspoäng och deras relation-om någon – gör någon mening i första hand. Vi skapar vårt diagram från grafer äldre dialoger Scatter/Dot och vi följer sedan skärmdumparna nedan.

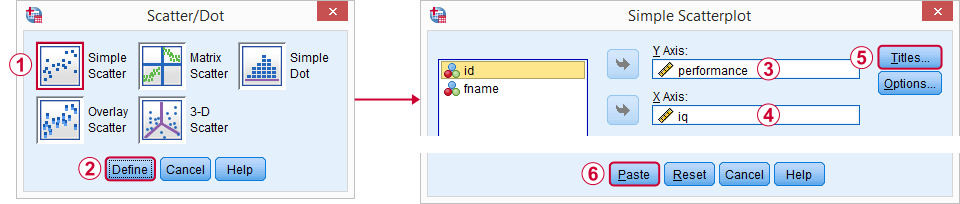
jag gillar personligen att kasta in

• en titel som säger vad min publik i princip tittar på och
• en undertext som säger vilka respondenter eller observationer som visas och hur många.

att gå igenom dialogrutorna resulterade i syntaxen nedan. Så låt oss köra det.

SPSS Scatterplot med titlar Syntax

resultat

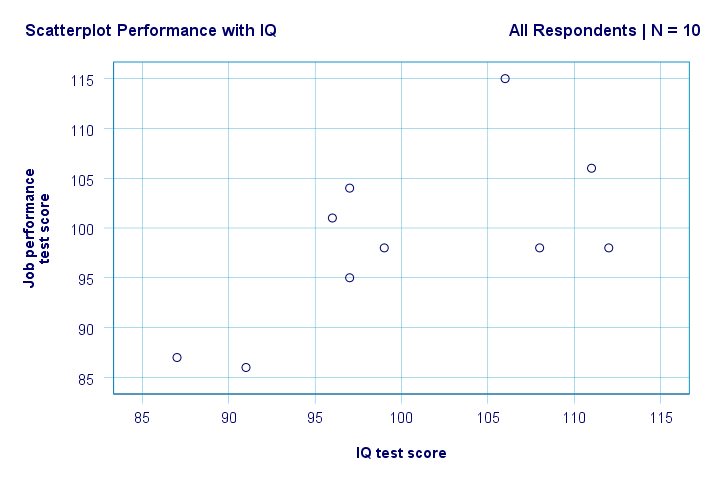
höger. Så först ser vi inte något konstigt i vår spridningsplot. Det verkar finnas en måttlig korrelation mellan IQ och prestanda: i genomsnitt verkar respondenter med högre IQ-poäng prestera bättre. Detta förhållande ser ungefär linjärt ut.
Låt oss nu lägga till en regressionslinje till vår scatterplot. Högerklicka på den och välj Redigera innehåll i separat fönster öppnas ett Diagramredigeringsfönster. Här klickar vi helt enkelt på ikonen” Lägg till anpassad linje vid Total ” som visas nedan.

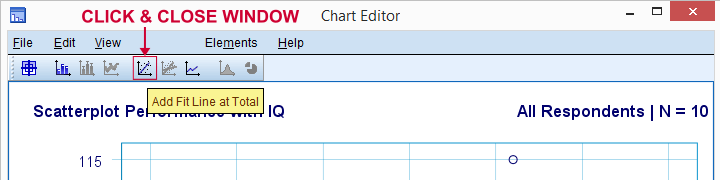
som standard lägger SPSS nu till en linjär regressionslinje till vår scatterplot. Resultatet visas nedan.

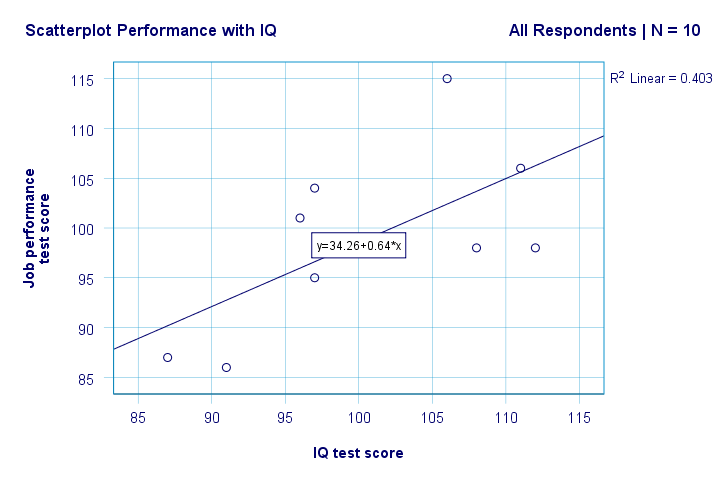
vi har nu några första grundläggande svar på våra forskningsfrågor. R2 = 0,403 indikerar att IQ står för cirka 40,3% av variansen i prestationspoäng. Det vill säga, IQ förutspår prestanda ganska bra i detta prov.
men hur kan vi bäst förutsäga jobbprestanda från IQ? Tja, i vår scatterplot är y prestanda (visas på y-axeln) och x är IQ (visas på x-axeln). Så det kommer att varaprestanda = 34,26 + 0,64 * IQ.So för en arbetssökande med en IQ-poäng på 115 kommer vi att förutsäga 34.26 + 0.64 * 115 = 107.86 som hans / hennes mest sannolika framtida prestationspoäng.
rätt, så det ger oss en grundläggande uppfattning om förhållandet mellan IQ och prestanda och presenterar det visuellt. Men mycket information – statistisk signifikans och konfidensintervall-saknas fortfarande. Så låt oss gå och hämta det.

SPSS linjär Regression dialogrutor

Rerunning vår minimal regressionsanalys från analysera Regression linjär ger oss mycket mer detaljerad utgång. Skärmdumparna nedan visar hur vi ska gå vidare.

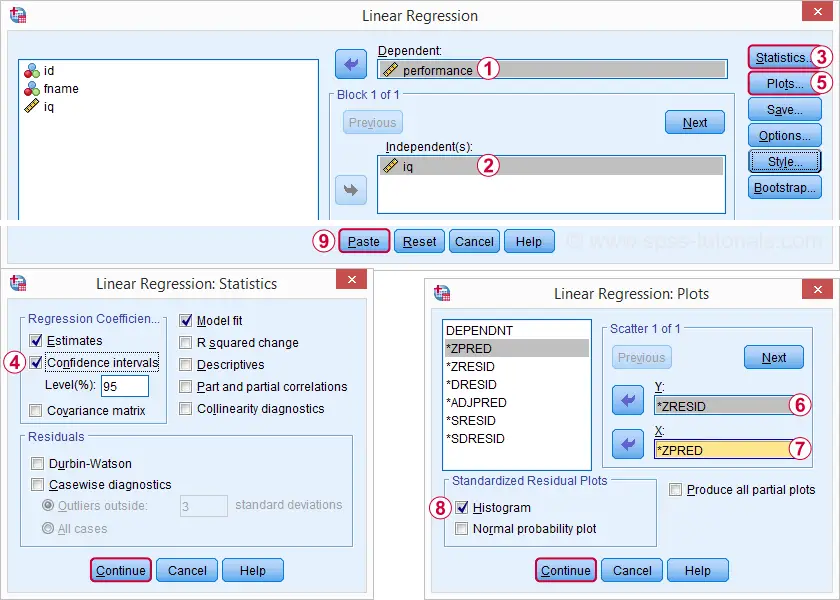
att välja dessa alternativ resulterar i syntaxen nedan. Vi kör det.

SPSS enkel linjär Regressionssyntax

SPSS Regressionsutgång I-koefficienter

tyvärr ger SPSS oss mycket mer regressionsutgång än vi behöver. Vi kan säkert ignorera det mesta. En tabell av stor betydelse är emellertid koefficienttabellen som visas nedan.

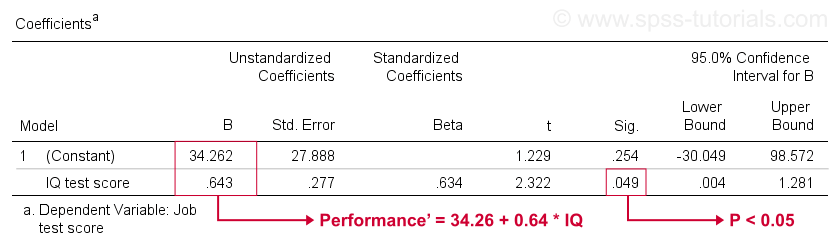
denna tabell visar de b-koefficienter som vi redan såg i vår scatterplot. Som angivet innebär Dessa den linjära regressionsekvationen som bäst uppskattar arbetsprestanda från IQ i vårt prov.
för det andra, kom ihåg att vi vanligtvis avvisar nollhypotesen om p < 0.05. B-koefficienten för IQ har ”Sig” eller p = 0,049. Det skiljer sig statistiskt signifikant från noll.
men dess 95% konfidensintervall-ungefär ett troligt intervall för dess befolkningsvärde – är . Så B är förmodligen inte noll men det kan mycket väl vara mycket nära noll. Konfidensintervallet är enormt – vår uppskattning för B är inte exakt alls-och detta beror på den minimala provstorleken som analysen bygger på.

SPSS Regression Output II-modellöversikt

bortsett från koefficienttabellen behöver vi också Modellöversiktstabellen för att rapportera våra resultat.

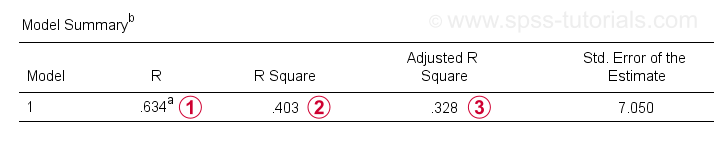
R är korrelationen mellan de förutspådda regressionsvärdena och de faktiska värdena. För enkel regression är R lika med korrelationen mellan prediktorn och beroende variabel.
R kvadrat-den kvadrerade korrelationen-indikerar andelen varians i den beroende variabeln som redovisas av prediktorn(erna) i våra provdata.
justerad R-kvadrat uppskattar R-kvadrat när vi tillämpar vår (provbaserade) regressionsekvation på hela befolkningen.
justerad R-kvadrat ger en mer realistisk uppskattning av prediktiv noggrannhet än bara r-kvadrat. I vårt exempel beror den stora skillnaden mellan dem-allmänt kallad krympning – på vår mycket minimala provstorlek på endast N = 10.
i alla fall är det dåliga nyheter för företag X: IQ förutspår inte riktigt jobbprestanda så snyggt trots allt.

utvärdering av Regressionsantagandena

huvudantagandena för regression är

1. oberoende observationer;
2. normalitet: fel måste följa en normalfördelning i befolkningen;
3. linjäritet: förhållandet mellan varje prediktor och den beroende variabeln är linjär;
4. Homoscedasticitet: fel måste ha konstant varians över alla nivåer av förutsagt värde.

1. Om varje fall (rad av celler i datavy) i SPSS representerar en separat person, antar vi vanligtvis att dessa är ”oberoende observationer”. Därefter utvärderas antaganden 2-4 bäst genom att inspektera regressionsplanerna i vår produktion.

2. Om normalitet håller, bör våra regressionsrester vara (ungefär) normalt fördelade. Histogrammet nedan visar inte en tydlig avvikelse från normalitet.

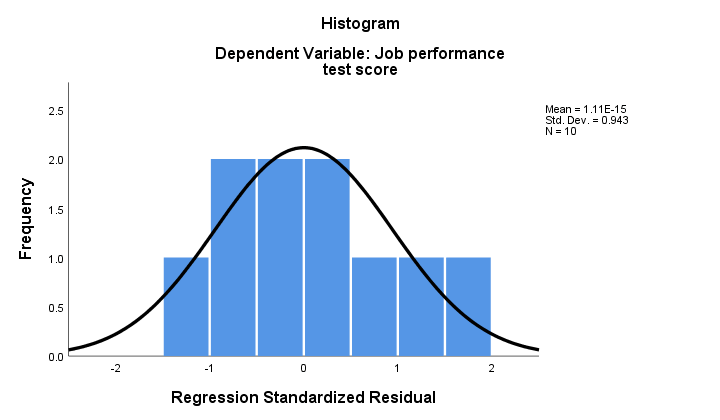
regressionsförfarandet kan lägga till dessa rester som en ny variabel till dina data. Genom att göra det kan du köra ett Kolmogorov-Smirnov-test för normalitet på dem. För det lilla provet till hands kommer dock detta test knappast att ha någon statistisk kraft. Så låt oss hoppa över det.

den 3. linjäritet och 4. homoscedasticitetsantaganden utvärderas bäst från en restplott. Detta är en scatterplot med förutsagda värden i x-axeln och rester på y-axeln som visas nedan. Båda variablerna har standardiserats men detta påverkar inte formen på prickmönstret.

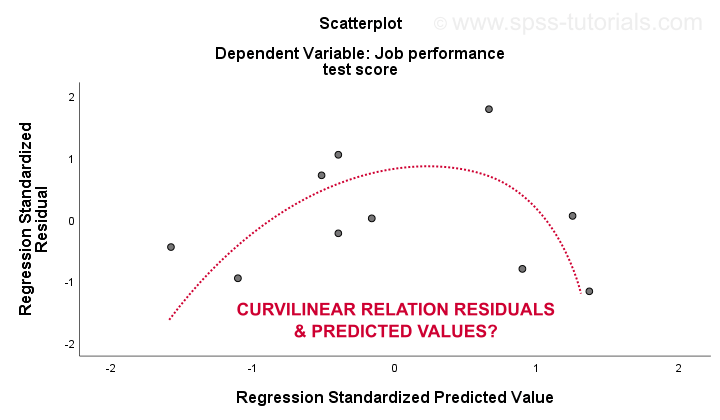
ärligt talat visar restplotten stark curvilinearity. Jag ritade manuellt kurvan som jag tycker passar bäst det övergripande mönstret. Om man antar en krökt relation löser förmodligen heteroscedasticiteten också men saker och ting blir alltför tekniska nu.Den grundläggande punkten är helt enkelt att vissa antaganden inte håller.De vanligaste lösningarna för dessa problem – från värsta till bästa-är

• ignorerar dessa antaganden helt och hållet;
• ljuger att regressionsplanerna inte indikerar några överträdelser av modellantagandena;
• en icke-linjär transformation – som logaritmisk-till den beroende variabeln;
• passar en krökt modell-som vi kommer att ge ett skott på en minut.

APA-riktlinjer för rapportering av Regression

figuren nedan är-ganska bokstavligen – en läroboksillustration för rapportering av regression i APA-format.

att skapa denna exakta tabell från SPSS-utgången är en verklig smärta i röven. Redigering Det går lättare i Excel än i WORD, så det kan spara dig åtminstone några problem.
Alternativt kan du försöka komma undan med att kopiera klistra in (oredigerad) SPSS-utdata och låtsas vara omedveten om det exakta APA-formatet.

icke-linjärt Regressionsexperiment

vår provstorlek är för liten för att verkligen passa något utöver en linjär modell. Men vi gjorde det ändå – bara nyfikenhet. Det enklaste alternativet i SPSS är under analysera Regression kurva uppskattning.Vi kommer inte att diskutera dialogrutorna men vi klistrade in syntaxen nedan.

SPSS icke-linjär Regressionssyntax

resultat

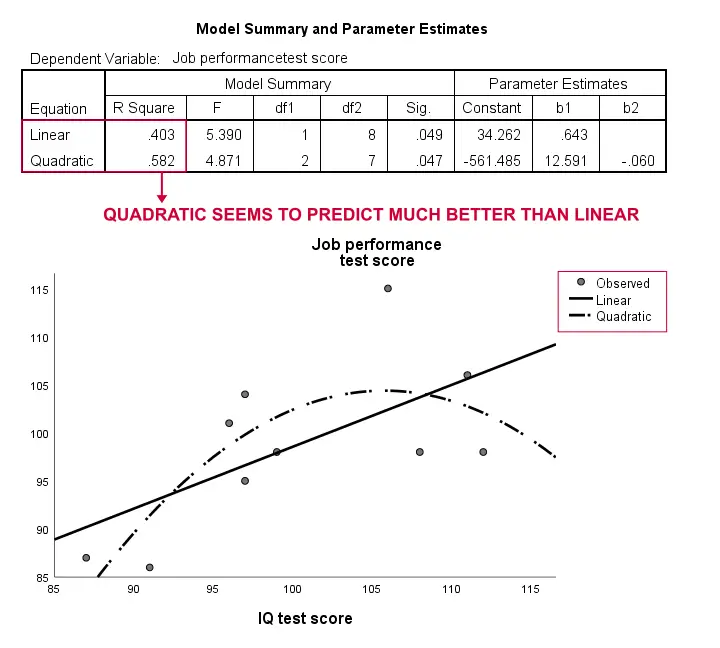
återigen är vårt prov alldeles för litet för att avsluta något allvarligt. Resultaten tyder dock på att en krökt modell passar våra data mycket bättre än den linjära. Vi kommer inte att utforska detta längre men vi ville nämna det; vi anser att krökta modeller rutinmässigt förbises av samhällsvetare.

Tack för att du läste!