SPSS Simple Linear Regression Tutorial
- Crea Scatterplot con Fit Line
- SPSS Linear Regression Dialogs
- Interpreting SPSS Regression Output
- Evaluating the Regression Assumptions
- APA Guidelines for Reporting Regression
Ricerca Domanda e dati
Società X aveva 10 dipendenti prendere un IQ e job performance test. I dati risultanti – parte dei quali sono mostrati di seguito-sono in regressione lineare semplice.sav.
La cosa principale che la società X vuole capire èil QI prevede le prestazioni del lavoro? E-se sì-come?Risponderemo a queste domande eseguendo una semplice analisi di regressione lineare in SPSS.
Crea Scatterplot con Fit Line
Un ottimo punto di partenza per la nostra analisi è un scatterplot. Questo ci dirà se il QI e i punteggi delle prestazioni e la loro relazione-se ce ne sono – hanno senso in primo luogo. Creeremo il nostro grafico da Grafici  Legacy Dialogs
Legacy Dialogs  Scatter / Dot e seguiremo gli screenshot qui sotto.
Scatter / Dot e seguiremo gli screenshot qui sotto.
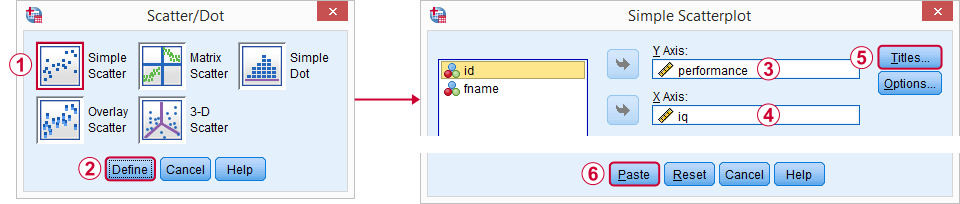
 Personalmente mi piace buttare dentro
Personalmente mi piace buttare dentro
- un titolo che dice ciò che il mio pubblico sta fondamentalmente guardando e
- un sottotitolo che dice quali intervistati o osservazioni sono mostrati e quanti.
Scorrendo le finestre di dialogo si ottiene la sintassi seguente. Quindi facciamolo.
SPSS Scatterplot con sintassi titoli
GRAPH
/SCATTERPLOT(BIVAR)=iq CON prestazioni
/MISSING=LISTWISE
/TITLE=’Scatterplot Performance con IQ’
| subtitle ‘All Responders / N = 10’.
Risultato
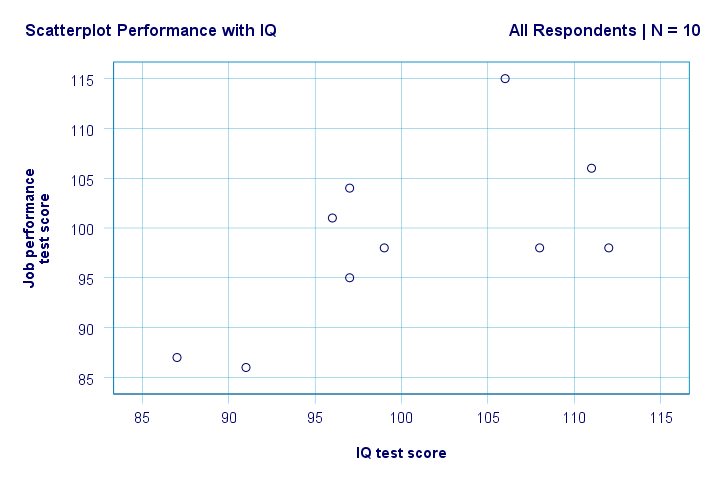
Destra. Quindi, prima di tutto, non vediamo nulla di strano nel nostro scatterplot. Sembra esserci una correlazione moderata tra QI e prestazioni: in media, gli intervistati con punteggi di QI più alti sembrano avere prestazioni migliori. Questa relazione sembra approssimativamente lineare.
Aggiungiamo ora una linea di regressione al nostro scatterplot. Facendo clic con il pulsante destro del mouse e selezionando Modifica contenuto  Nella finestra separata si apre una finestra dell’editor di grafici. Qui è sufficiente fare clic sull’icona” Aggiungi linea adatta al totale ” come mostrato di seguito.
Nella finestra separata si apre una finestra dell’editor di grafici. Qui è sufficiente fare clic sull’icona” Aggiungi linea adatta al totale ” come mostrato di seguito.
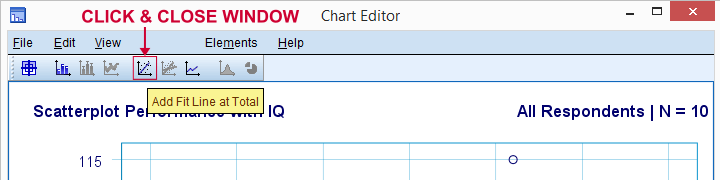
Per impostazione predefinita, SPSS ora aggiunge una linea di regressione lineare al nostro scatterplot. Il risultato è mostrato di seguito.
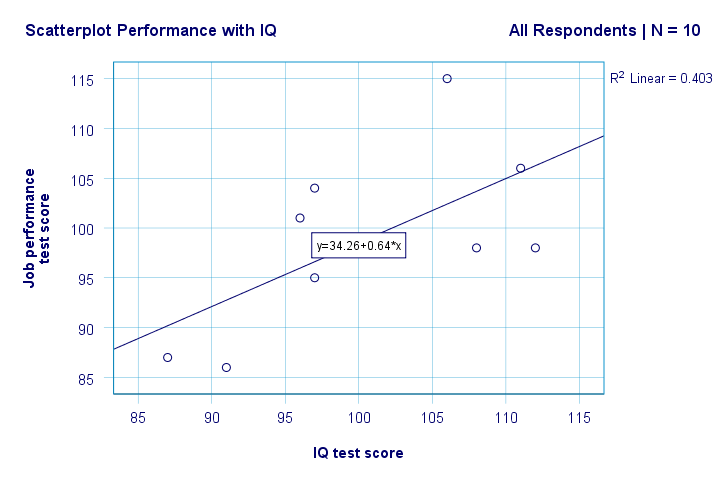
Ora abbiamo alcune prime risposte di base alle nostre domande di ricerca. R2 = 0,403 indica che IQ rappresenta circa il 40,3% della varianza nei punteggi delle prestazioni. Cioè, IQ predice le prestazioni abbastanza bene in questo campione.
Ma come possiamo prevedere al meglio le prestazioni lavorative da IQ? Bene, nel nostro scatterplot y è la prestazione (mostrata sull’asse y) e x è IQ (mostrato sull’asse x). Quindi beperformance = 34.26 + 0.64 * IQ.So per un candidato di lavoro con un punteggio IQ di 115, prevederemo 34.26 + 0.64 * 115 = 107.86 come il suo / il suo punteggio più probabile prestazioni future.
Giusto, in modo che ci dà un’idea di base circa la relazione tra IQ e prestazioni e lo presenta visivamente. Tuttavia, molte informazioni-significatività statistica e intervalli di confidenza – mancano ancora. Quindi andiamo a prenderlo.
Finestre di dialogo di regressione lineare SPSS
Rieseguendo la nostra analisi di regressione minima da Analyze  Regression
Regression  Linear ci offre un output molto più dettagliato. Gli screenshot qui sotto mostrano come procederemo.
Linear ci offre un output molto più dettagliato. Gli screenshot qui sotto mostrano come procederemo.
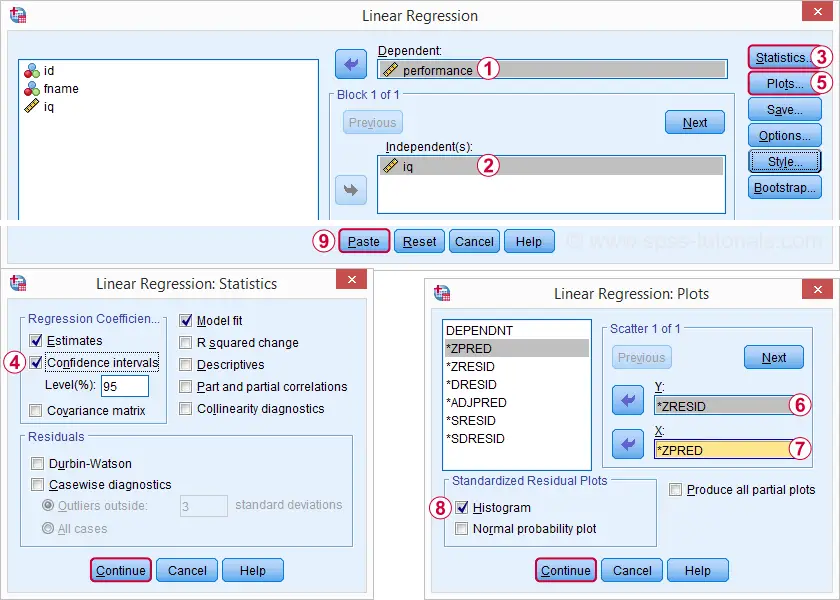
Selezionando queste opzioni si ottiene la seguente sintassi. Facciamolo.
SPSS Sintassi di regressione lineare semplice
REGRESSIONE
/MANCANTE LISTWISE
/STATISTICHE COEFF OUT CI(95) R ANOVA
/CRITERI=PIN(.05) BRONCIO(.10)
/NOORIGIN
/Prestazioni DIPENDENTI
/METHOD=INSERISCI iq
/SCATTERPLOT=(*ZRESID ,*ZPRED)
/ ISTOGRAMMA DEI RESIDUI(ZRESID).
SPSS Regression Output I – Coefficients
Sfortunatamente, SPSS ci dà molto più output di regressione di cui abbiamo bisogno. Possiamo tranquillamente ignorarne la maggior parte. Tuttavia, una tabella di grande importanza è la tabella dei coefficienti mostrata di seguito.
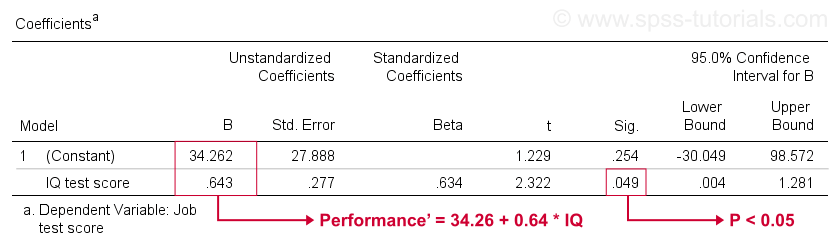
Questa tabella mostra i coefficienti B che abbiamo già visto nel nostro scatterplot. Come indicato, questi implicano l’equazione di regressione lineare che stima al meglio le prestazioni del lavoro dal QI nel nostro campione.
In secondo luogo, ricorda che di solito rifiutiamo l’ipotesi nulla se p < 0.05. Il coefficiente B per IQ ha ” Sig ” o p = 0,049. È statisticamente significativamente diverso da zero.
Tuttavia, il suo intervallo di confidenza del 95%- approssimativamente, un intervallo probabile per il suo valore di popolazione – è . Quindi B probabilmente non è zero ma potrebbe essere molto vicino a zero. L’intervallo di confidenza è enorme -la nostra stima per B non è affatto precisa-e ciò è dovuto alla dimensione minima del campione su cui si basa l’analisi.
SPSS Regression Output II – Model Summary
Oltre alla tabella dei coefficienti, abbiamo anche bisogno della tabella di riepilogo del modello per riportare i nostri risultati.
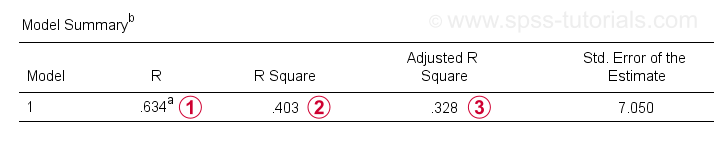
 R è la correlazione tra i valori previsti di regressione e i valori effettivi. Per la regressione semplice, R è uguale alla correlazione tra il predittore e la variabile dipendente.
R è la correlazione tra i valori previsti di regressione e i valori effettivi. Per la regressione semplice, R è uguale alla correlazione tra il predittore e la variabile dipendente.
 R Square-la correlazione al quadrato – indica la proporzione di varianza nella variabile dipendente rappresentata dai predittori nei nostri dati di esempio.
R Square-la correlazione al quadrato – indica la proporzione di varianza nella variabile dipendente rappresentata dai predittori nei nostri dati di esempio.
 R-square rettificato stima R-square quando si applica la nostra equazione di regressione (basata su campione) all’intera popolazione.
R-square rettificato stima R-square quando si applica la nostra equazione di regressione (basata su campione) all’intera popolazione.
r-square rettificato fornisce una stima più realistica dell’accuratezza predittiva rispetto al semplice r-square. Nel nostro esempio, la grande differenza tra loro-generalmente indicata come restringimento-è dovuta alla nostra dimensione minima del campione di soli N = 10.
In ogni caso, questa è una cattiva notizia per la società X: IQ non prevede davvero le prestazioni del lavoro così bene dopo tutto.
Valutazione delle ipotesi di regressione
Le ipotesi principali per la regressione sono
- Osservazioni indipendenti;
- Normalità: gli errori devono seguire una distribuzione normale nella popolazione;
- Linearità: la relazione tra ciascun predittore e la variabile dipendente è lineare;
- Omoscedasticità: gli errori devono avere varianza costante su tutti i livelli di valore previsto.
1. Se ogni caso (riga di celle nella vista dati) in SPSS rappresenta una persona separata, di solito assumiamo che queste siano “osservazioni indipendenti”. Successivamente, le ipotesi 2-4 vengono valutate al meglio ispezionando i grafici di regressione nel nostro output.
2. Se la normalità tiene, allora i nostri residui di regressione dovrebbero essere (approssimativamente) distribuiti normalmente. L’istogramma qui sotto non mostra una chiara partenza dalla normalità.
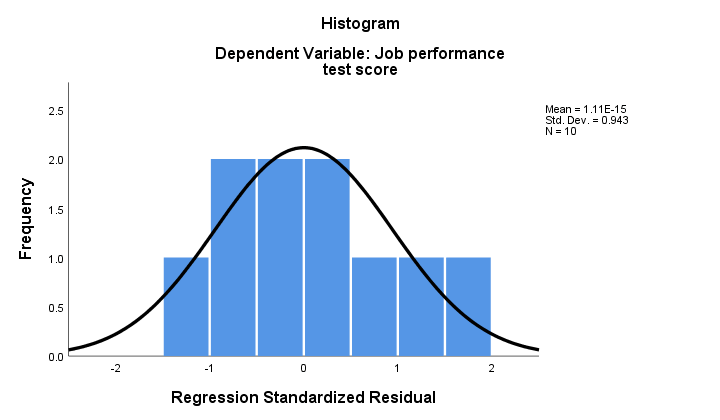
La procedura di regressione può aggiungere questi residui come una nuova variabile ai dati. In questo modo, è possibile eseguire un test Kolmogorov-Smirnov per la normalità su di loro. Per il piccolo campione a portata di mano, tuttavia, questo test difficilmente avrà alcun potere statistico. Quindi saltiamola.
Il 3. linearità e 4. le ipotesi di omoscedasticità sono valutate al meglio da una trama residua. Questo è un grafico a dispersione con valori previsti nell’asse x e residui sull’asse y come mostrato di seguito. Entrambe le variabili sono state standardizzate ma ciò non influisce sulla forma del modello di punti.
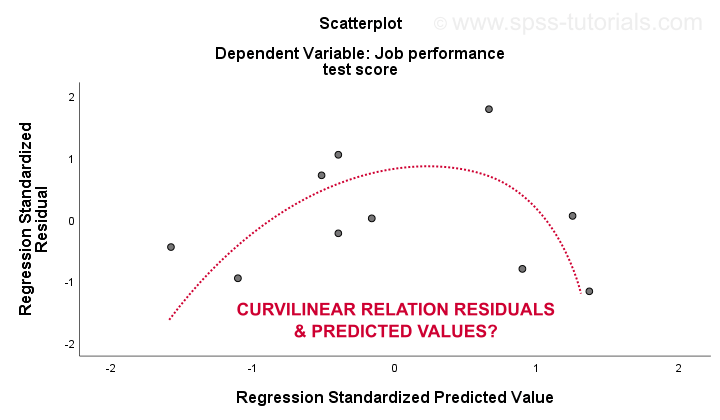
Onestamente, la trama residua mostra una forte curvilinearità. Ho disegnato manualmente la curva che penso si adatti meglio al modello generale. Supponendo una relazione curvilinea probabilmente risolve anche l’eteroscedasticità, ma ora le cose stanno diventando troppo tecniche.Il punto di base è semplicemente che alcune ipotesi non reggono.Le più comuni soluzioni per questi problemi -dal peggiore al migliore – sono
- ignorando questi presupposti del tutto;
- sdraiato che la regressione trame non indicare eventuali violazioni del modello di ipotesi;
- non trasformazione lineare -come logaritmica – per la variabile dipendente;
- raccordo curvilineo modello -che daremo un colpo in un minuto.
Linee guida APA per la segnalazione di regressione
La figura seguente è-letteralmente – un’illustrazione da manuale per la segnalazione di regressione in formato APA.

Creare questa tabella esatta dall’output SPSS è un vero rompicapo. La modifica è più facile in Excel che in WORD, in modo che possa farti risparmiare almeno qualche problema.
In alternativa, prova a farla franca copiando l’output SPSS (inedito) e fingi di non essere a conoscenza del formato APA esatto.
Esperimento di regressione non lineare
La nostra dimensione del campione è troppo piccola per adattarsi davvero a qualsiasi cosa al di là di un modello lineare. Ma lo abbiamo fatto comunque – solo curiosità. L’opzione più semplice in SPSS è sotto Analizza  Regressione
Regressione  Stima della curva.Non stiamo andando a discutere le finestre di dialogo, ma abbiamo incollato la sintassi qui sotto.
Stima della curva.Non stiamo andando a discutere le finestre di dialogo, ma abbiamo incollato la sintassi qui sotto.
SPSS Sintassi di regressione non lineare
TSET NEWVAR = NONE.
CURVEFIT
/VARIABILI=prestazioni CON iq
/COSTANTE
/MODELLO= lineare quadratico
/ PLOT FIT.
Risultati
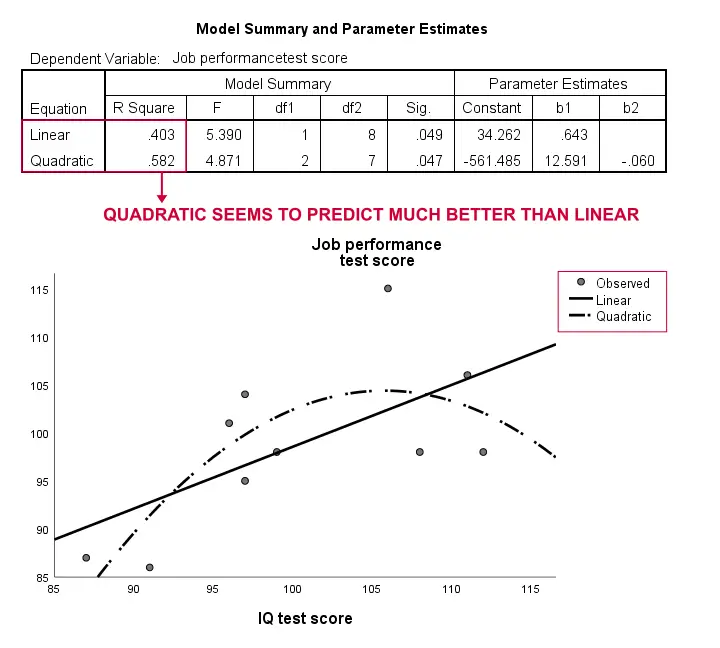
Ancora una volta, il nostro campione è troppo piccolo per concludere qualcosa di serio. Tuttavia, i risultati suggeriscono che un modello curvilineo si adatta ai nostri dati molto meglio di quello lineare. Non esploreremo ulteriormente questo, ma volevamo menzionarlo; riteniamo che i modelli curvilinei siano abitualmente trascurati dagli scienziati sociali.
Grazie per la lettura!




