SPSS simplu tutorial regresie liniară
- creați Scatterplot cu linia de potrivire
- Dialoguri de regresie liniară SPSS
- interpretarea ieșirii de regresie SPSS
- evaluarea ipotezelor de regresie
- ghidurile APA pentru raportarea regresiei
întrebare de cercetare și date
Compania X a avut 10 angajați să ia un test de IQ și de performanță de locuri de muncă. Datele rezultate-o parte din care sunt prezentate mai jos – sunt în regresie simplă-liniară.sav.
principalul lucru pe care Compania X vrea să-l descopere este IQ prezice performanța locului de muncă? Și-dacă da-cum?Vom răspunde la aceste întrebări rulând o simplă analiză de regresie liniară în SPSS.
creați Scatterplot cu linia Fit
un punct de plecare excelent pentru analiza noastră este un scatterplot. Acest lucru ne va spune dacă IQ-ul și scorurile de performanță și relația lor – dacă există-au vreun sens în primul rând. Vom crea graficul nostru din grafice  Legacy Dialogs
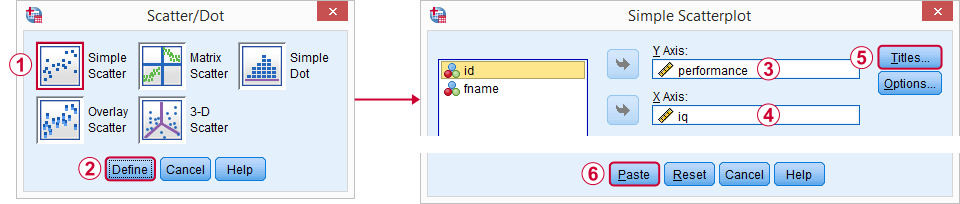
Legacy Dialogs  Scatter/Dot și apoi vom urmări capturile de ecran de mai jos.
Scatter/Dot și apoi vom urmări capturile de ecran de mai jos.
 eu personal place să arunce în
eu personal place să arunce în
- un titlu care spune la ce se uită publicul meu și
- un subtitlu care spune ce respondenți sau observații sunt afișate și câte.
trecerea prin dialoguri a dus la sintaxa de mai jos. Deci, să-l rulați.
SPSS Scatterplot cu sintaxa titlurilor
grafic
/ SCATTERPLOT(BIVAR)=iq cu performanță
/lipsă=LISTWISE
/TITLE = ‘performanță Scatterplot cu IQ’
/subtitrare ‘toți respondenții | N = 10’.
rezultat
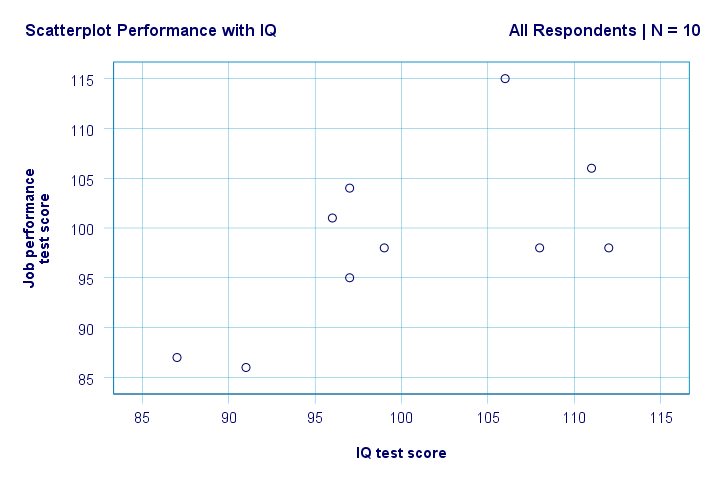
dreapta. Deci, în primul rând, nu vedem nimic ciudat în scatterplot nostru. Se pare că există o corelație moderată între IQ și performanță: în medie, respondenții cu scoruri IQ mai mari par să aibă performanțe mai bune. Această relație pare aproximativ liniară.
să adăugăm acum o linie de regresie la scatterplot-ul nostru. Făcând clic dreapta pe acesta și selectând Editare conținut  în fereastră separată se deschide o fereastră Editor Diagramă. Aici pur și simplu facem clic pe pictograma „Adăugați linia potrivită la Total”, așa cum se arată mai jos.
în fereastră separată se deschide o fereastră Editor Diagramă. Aici pur și simplu facem clic pe pictograma „Adăugați linia potrivită la Total”, așa cum se arată mai jos.
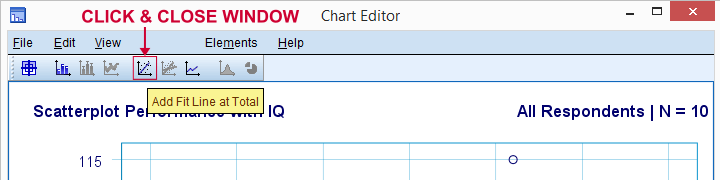
în mod implicit, SPSS adaugă acum o linie de regresie liniară la scatterplot-ul nostru. Rezultatul este prezentat mai jos.
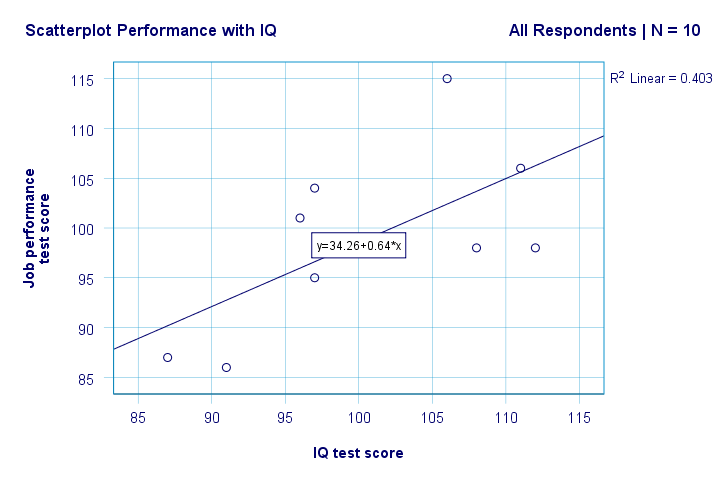
avem acum câteva răspunsuri de bază la întrebările noastre de cercetare. R2 = 0,403 indică faptul că IQ reprezintă aproximativ 40,3% din variația scorurilor de performanță. Adică, IQ prezice performanța destul de bine în acest eșantion.
dar cum putem prezice cel mai bine performanța locului de muncă din IQ? Ei bine, în scatterplot-ul nostru y este performanța (afișată pe axa y) și x este IQ (afișată pe axa x). Deci asta va fiperformanță = 34.26 + 0.64 * IQ.So pentru un solicitant de locuri de muncă cu un scor IQ de 115, vom prezice 34.26 + 0.64 * 115 = 107.86 ca cel mai probabil scor de performanță viitor.
corect, așa că ne oferă o idee de bază despre relația dintre IQ și performanță și o prezintă vizual. Cu toate acestea, o mulțime de informații-semnificație statistică și intervale de încredere – încă lipsesc. Deci, să mergem și să-l.
Dialoguri de regresie liniară SPSS
reluând analiza noastră de regresie minimă din analiza regresia
regresia Linear ne oferă o ieșire mult mai detaliată. Capturile de ecran de mai jos arată cum vom proceda.
Linear ne oferă o ieșire mult mai detaliată. Capturile de ecran de mai jos arată cum vom proceda.
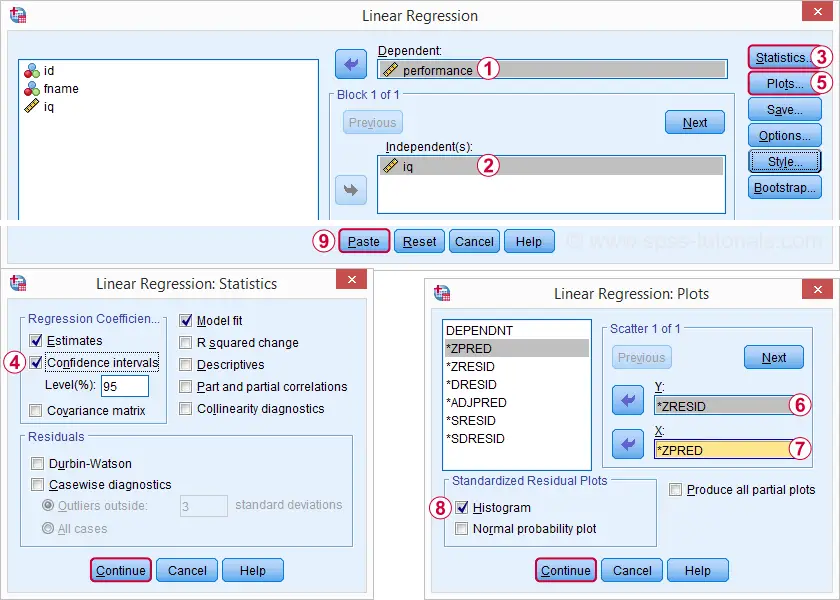
selectarea acestor opțiuni are ca rezultat sintaxa de mai jos. Să-l rulați.
SPSS simplă sintaxă de regresie liniară
REGRESIE
/ LIPSĂ LISTWISE
/STATISTICI COEFF OUTS CI(95) R ANOVA
/CRITERII=PIN(.05) merluciu(.10)
/NOORIGIN
/performanță dependentă
/metodă=introduceți iq
/SCATTERPLOT=(*ZRESID ,*ZPRED)
/histograma reziduurilor(ZRESID).
ieșire de regresie SPSS i – coeficienți
din păcate, SPSS ne oferă mult mai multă ieșire de regresie decât avem nevoie. Putem ignora în siguranță cea mai mare parte. Cu toate acestea, un tabel de importanță majoră este tabelul coeficienților prezentat mai jos.
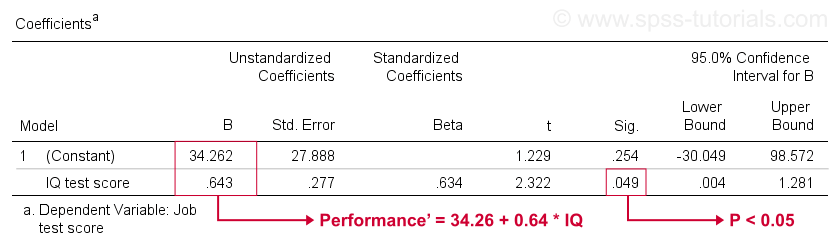
acest tabel prezintă coeficienții B pe care i-am văzut deja în scatterplot-ul nostru. După cum s-a indicat, acestea implică ecuația de regresie liniară care estimează cel mai bine performanța locului de muncă din IQ în eșantionul nostru.
în al doilea rând, amintiți-vă că de obicei respingem ipoteza nulă dacă p < 0,05. Coeficientul B pentru IQ are „Sig” sau p = 0,049. Este semnificativ statistic diferit de zero.
cu toate acestea, intervalul său de încredere de 95%- aproximativ, un interval probabil pentru valoarea populației sale – este . Deci B nu este probabil zero, dar poate fi foarte aproape de zero. Intervalul de încredere este imens-estimarea noastră pentru B nu este deloc precisă – și acest lucru se datorează dimensiunii minime a eșantionului pe care se bazează analiza.
ieșire de regresie SPSS II – rezumat Model
în afară de tabelul coeficienților, avem nevoie și de tabelul rezumat Model pentru raportarea rezultatelor noastre.
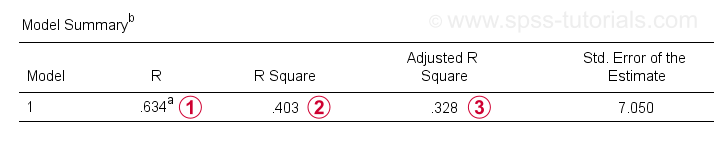
 R este corelația dintre valorile prezise de regresie și valorile reale. Pentru regresia simplă, R este egal cu corelația dintre predictor și variabila dependentă.
R este corelația dintre valorile prezise de regresie și valorile reale. Pentru regresia simplă, R este egal cu corelația dintre predictor și variabila dependentă.
 R pătrat-corelația pătrat – indică proporția de varianță în variabila dependentă care este reprezentat de predictor(e) în datele noastre eșantion.
R pătrat-corelația pătrat – indică proporția de varianță în variabila dependentă care este reprezentat de predictor(e) în datele noastre eșantion.
 estimări R-pătrat ajustate R-pătrat atunci când se aplică ecuația noastră de regresie (bazată pe eșantion) la întreaga populație.
estimări R-pătrat ajustate R-pătrat atunci când se aplică ecuația noastră de regresie (bazată pe eșantion) la întreaga populație.
R-pătrat ajustat oferă o estimare mai realistă a preciziei predictive decât pur și simplu R-pătrat. În exemplul nostru, Diferența mare dintre ele-denumită în general contracție – se datorează dimensiunii noastre foarte minime a eșantionului de numai N = 10.
în orice caz, aceasta este o veste proastă pentru compania X: IQ nu prezice cu adevărat performanța locului de muncă atât de frumos până la urmă.
evaluarea ipotezelor de regresie
principalele ipoteze pentru regresie sunt
- observații independente;
- normalitate: erorile trebuie să urmeze o distribuție normală în populație;
- liniaritate: relația dintre fiecare predictor și variabila dependentă este liniară;
- Homoscedasticitate: erorile trebuie să aibă o variație constantă pe toate nivelurile valorii prezise.
1. Dacă fiecare caz (rând de celule în vizualizarea datelor) din SPSS reprezintă o persoană separată, de obicei presupunem că acestea sunt „observații independente”. Apoi, ipotezele 2-4 sunt cel mai bine evaluate prin inspectarea parcelelor de regresie din producția noastră.
2. Dacă normalitatea se menține, atunci reziduurile noastre de regresie ar trebui să fie (aproximativ) distribuite în mod normal. Histograma de mai jos nu arată o abatere clară de la normalitate.
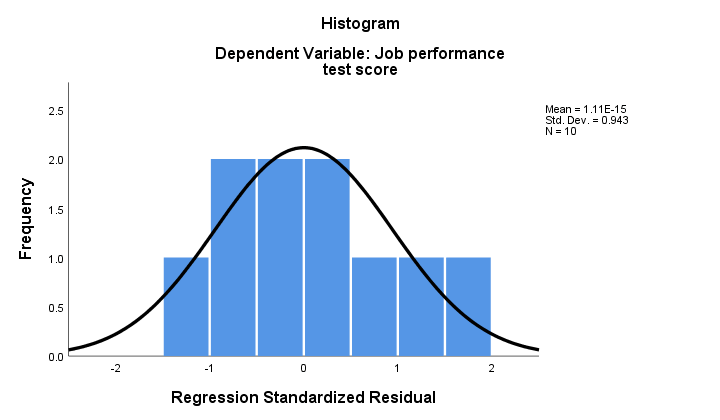
procedura de regresie poate adăuga aceste reziduuri ca o nouă variabilă la datele dvs. Procedând astfel, ați putea rula un test Kolmogorov-Smirnov pentru normalitate asupra lor. Cu toate acestea, pentru eșantionul mic la îndemână, acest test nu va avea cu greu nicio putere statistică. Așa că hai să sărim peste asta.
3. liniaritate și 4. ipotezele de homoscedasticitate sunt cel mai bine evaluate dintr-un complot rezidual. Acesta este un scatterplot cu valori prezise în axa x și reziduuri pe axa y așa cum se arată mai jos. Ambele variabile au fost standardizate, dar acest lucru nu afectează forma modelului de puncte.
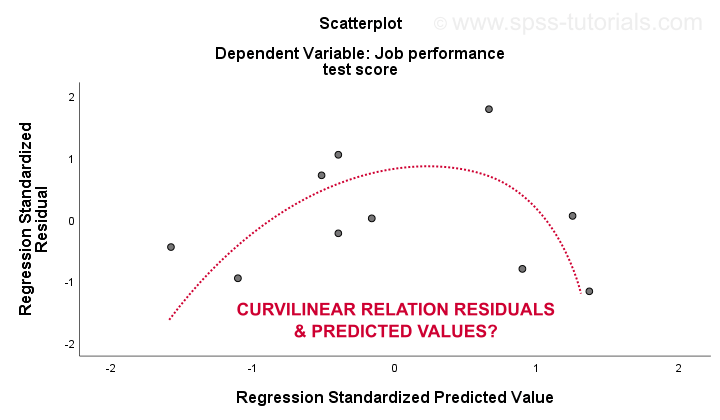
sincer, graficul rezidual prezinta curbilinearity puternic. Am desenat manual curba care cred că se potrivește cel mai bine modelului general. Presupunând că o relație curbilinie rezolvă probabil și heteroscedasticitatea, dar lucrurile devin mult prea tehnice acum.Punctul de bază este pur și simplu că unele ipoteze nu dețin.Cele mai comune soluții pentru aceste probleme-de la cel mai rău la cel mai bun – sunt
- ignorarea acestor ipoteze cu totul;
- minciuna că parcelele de regresie nu indică nicio încălcare a ipotezelor modelului;
- o transformare neliniară-cum ar fi logaritmică – la variabila dependentă;
- montarea unui model curbiliniu-pe care îl vom da într-un minut.
instrucțiuni APA pentru raportarea regresiei
figura de mai jos este-literalmente – o ilustrare de manual pentru raportarea regresiei în format APA.

crearea acestui tabel exact din ieșirea SPSS este o adevărată durere în fund. Editarea merge mai ușor în Excel decât în WORD, astfel încât s-ar putea salva o cel puțin unele probleme.
alternativ, încercați să scăpați cu copierea-lipirea ieșirii SPSS (needitate) și pretindeți că nu știți exact formatul APA.
experiment de regresie neliniară
dimensiunea eșantionului nostru este prea mică pentru a se potrivi cu adevărat cu ceva dincolo de un model liniar. Dar am făcut-o oricum-doar curiozitate. Cea mai simplă opțiune în SPSS este sub analiza  regresie
regresie  curba estimare.Nu vom discuta dialogurile, dar am lipit sintaxa de mai jos.
curba estimare.Nu vom discuta dialogurile, dar am lipit sintaxa de mai jos.
Sintaxa de regresie neliniară SPSS
TSET NEWVAR=NICI UNUL.
CURVEFIT
/variabile=performanță cu iq
/constantă
/MODEL= liniar pătratic
/ potrivire complot.
rezultate
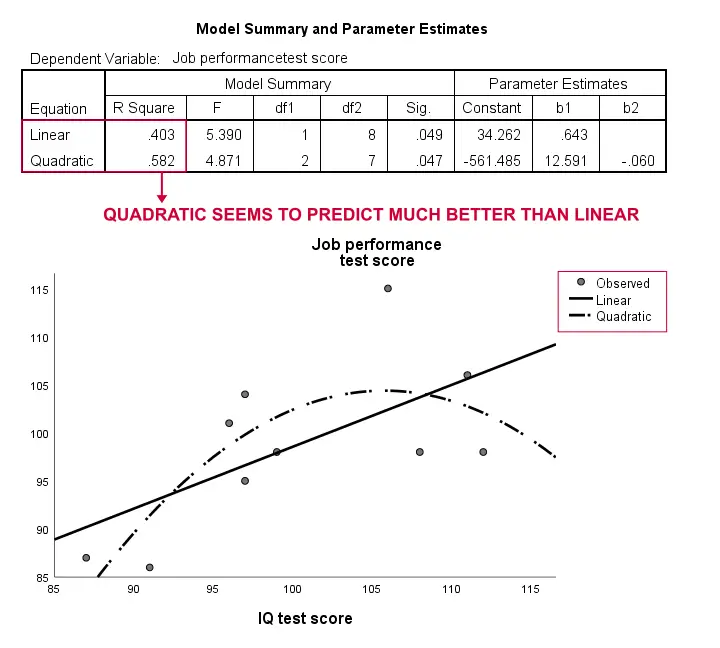
din nou, eșantionul nostru este mult prea mic pentru a concluziona ceva serios. Cu toate acestea, rezultatele sugerează că un model curbiliniu se potrivește mult mai bine datelor noastre decât cel liniar. Nu vom explora acest lucru mai departe, dar am vrut să-l menționăm; simțim că modelele curbilinii sunt trecute cu vederea în mod obișnuit de oamenii de știință sociali.
Vă mulțumim pentru lectură!




