SPSS Regressão Linear Simples Tutorial

SPSS Regressão Linear Simples Tutorial

1. Criar um gráfico de dispersão com a Linha de Ajuste
2. SPSS Regressão Linear caixas de diálogo
3. Interpretação SPSS Output da Regressão
4. Avaliar a Regressão Pressupostos
5. APA Diretrizes para Relatórios de Regressão

Pergunta de Pesquisa, e Dados

A empresa X tinha 10 os empregados tenham um QI de trabalho e de teste de desempenho. Os dados resultantes-parte dos quais são mostrados abaixo – estão em regressão linear simples.sav.

a principal coisa que a Empresa X quer descobrir éo QI prediz o desempenho do trabalho? E-se sim – como?Responderemos a essas perguntas executando uma análise de regressão linear simples no SPSS.

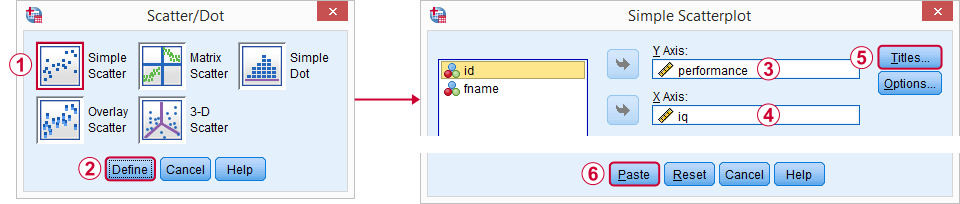
criar Scatterplot com linha de ajuste

um ótimo ponto de partida para nossa análise é um scatterplot. Isso nos dirá se o QI e as pontuações de desempenho e sua relação-se houver – fazem algum sentido em primeiro lugar. Criaremos nosso gráfico a partir de gráficos diálogos legados Scatter/Dot e seguiremos as capturas de tela abaixo.

eu, pessoalmente, gostaria de jogar no

• um título que diz o que o meu público-alvo são, basicamente, olhando e
• um subtítulo que diz que os entrevistados ou observações são mostradas e como muitos.

caminhar pelos diálogos resultou na sintaxe abaixo. Então vamos executá-lo.

SPSS Scatterplot with Titles Syntax

resultado

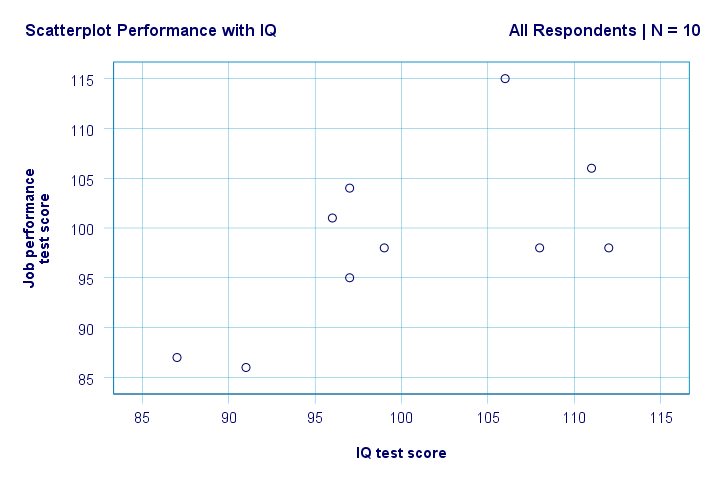
à direita. Então, primeiro, não vemos nada de estranho em nosso gráfico de dispersão. Parece haver uma correlação moderada entre QI e desempenho: em média, os entrevistados com pontuações de QI mais altas parecem ter um desempenho melhor. Essa relação parece aproximadamente linear.
vamos agora adicionar uma linha de regressão ao nosso gráfico de dispersão. Clicar com o botão direito do mouse e selecionar Editar conteúdo em uma janela separada abre uma janela do editor de gráficos. Aqui, basta clicar no ícone” Adicionar linha de ajuste no Total”, conforme mostrado abaixo.

por padrão, SPSS agora adiciona uma linha de regressão linear ao nosso scatterplot. O resultado é mostrado abaixo.

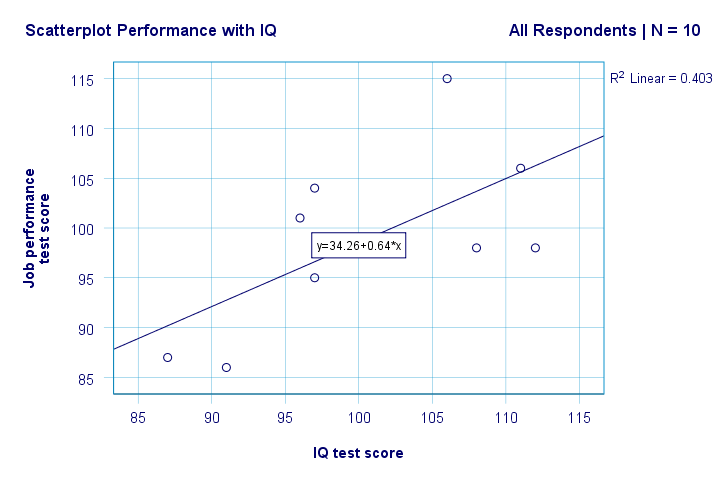
agora temos algumas primeiras respostas básicas para nossas perguntas de pesquisa. R2 = 0,403 indica que o QI representa cerca de 40,3% da variância nos escores de desempenho. Ou seja, o QI prevê desempenho bastante bem nesta amostra.
mas como podemos prever melhor o desempenho no trabalho a partir do QI? Bem, em nosso gráfico de dispersão y está o desempenho (mostrado no eixo y) e x é QI (mostrado no eixo x). Portanto, esse desempenho será = 34,26 + 0,64 * IQ.So para um candidato a emprego com uma pontuação de QI de 115, preveremos 34.26 + 0.64 * 115 = 107.86 como sua pontuação de desempenho futuro mais provável.
certo, então isso nos dá uma ideia básica sobre a relação entre QI e desempenho e a apresenta visualmente. No entanto, muitas informações-significância estatística e intervalos de confiança – ainda estão faltando. Então vamos buscá-lo.

SPSS Linear Regression Dialogs

Executar novamente nossa análise de regressão mínima a partir de Analyze Regression Linear nos dá uma saída muito mais detalhada. As imagens abaixo mostram como vamos proceder.

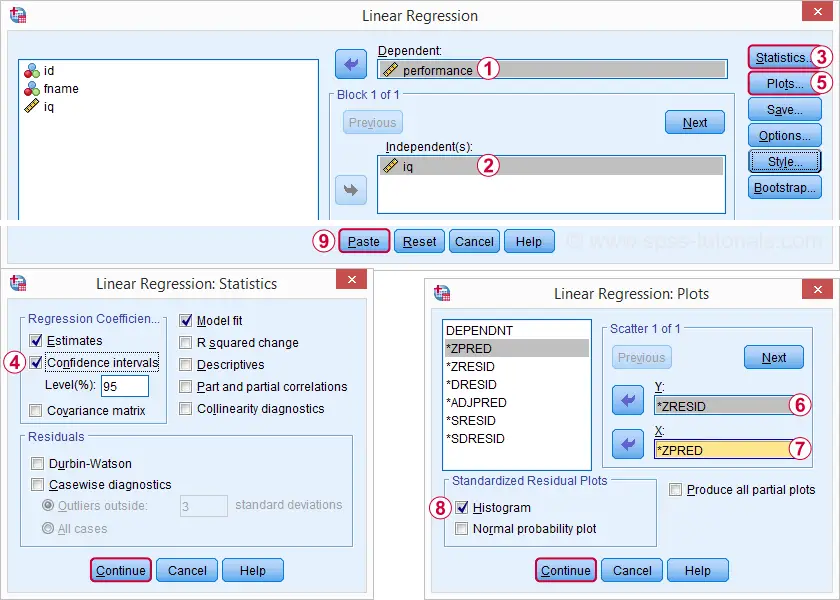
selecionar essas opções resulta na sintaxe abaixo. Vamos lá.

sintaxe de regressão Linear simples SPSS

saída de regressão SPSS I – coeficientes

Infelizmente, o SPSS nos dá muito mais saída de regressão do que precisamos. Podemos seguramente ignorar a maior parte disso. No entanto, uma tabela de grande importância é a tabela de coeficientes mostrada abaixo.

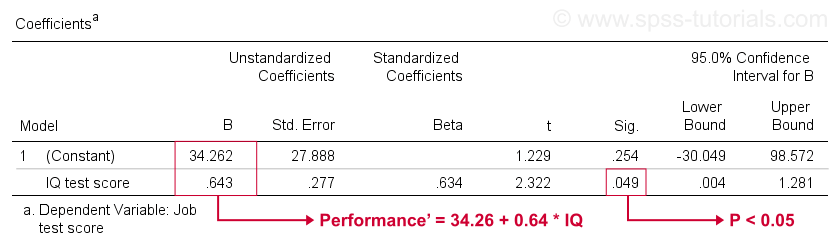
esta tabela mostra os coeficientes B que já vimos em nosso gráfico de dispersão. Conforme indicado, isso implica a equação de regressão linear que melhor estima o desempenho do trabalho a partir do QI em nossa amostra.
em segundo lugar, lembre-se de que geralmente rejeitamos a hipótese nula se p < 0,05. O coeficiente B para QI tem” Sig ” ou p = 0,049. É estatisticamente significativamente diferente de zero.No entanto, seu intervalo de confiança de 95%- aproximadamente, um intervalo provável para seu valor populacional – é . Portanto, B provavelmente não é zero, mas pode muito bem ser muito próximo de zero. O intervalo de confiança é enorme-nossa estimativa para B não é precisa – e isso se deve ao tamanho mínimo da amostra em que a análise se baseia.

saída de regressão SPSS II-Resumo do modelo

além da tabela de coeficientes, também precisamos da tabela de Resumo do modelo para relatar nossos resultados.

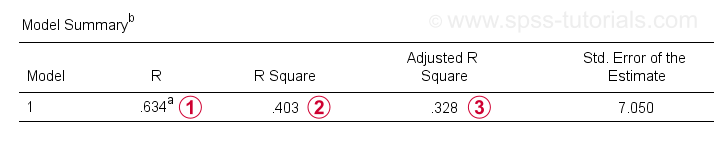
R é a correlação entre os valores previstos de regressão e os valores reais. Para regressão simples, R é igual à correlação entre o preditor e a variável dependente.
R Square – a correlação quadrada-indica a proporção de variância na variável dependente que é contabilizada pelo(s) preditor (s) em nossos dados de amostra.
estimativas ajustadas do quadrado R R-quadrado ao aplicar nossa equação de regressão (baseada em amostra) a toda a população.
o quadrado R ajustado fornece uma estimativa mais realista da precisão preditiva do que simplesmente o quadrado R. Em nosso exemplo, a grande diferença entre eles – geralmente referida como encolhimento-é devido ao nosso tamanho de amostra mínimo de apenas n = 10.
em qualquer caso, esta é uma má notícia para a Empresa X: IQ realmente não prevê o desempenho do trabalho tão bem depois de tudo.

Avaliar a Regressão Pressupostos

Os principais pressupostos para a regressão

1. observações Independentes;
2. Normalidade: os erros seguem uma distribuição normal na população;
3. linearidade: a relação entre cada preditor e a variável dependente é linear;
4. Homocedasticidade: os erros devem ter variância constante em todos os níveis do valor previsto.

1. Se cada caso (linha de células na visualização de dados) no SPSS representa uma pessoa separada, geralmente assumimos que essas são “observações independentes”. Em seguida, as suposições 2-4 São melhor avaliadas inspecionando os gráficos de regressão em nossa saída.

2. Se a normalidade se mantiver, então nossos resíduos de regressão devem ser (aproximadamente) normalmente distribuídos. O histograma abaixo não mostra um afastamento claro da normalidade.

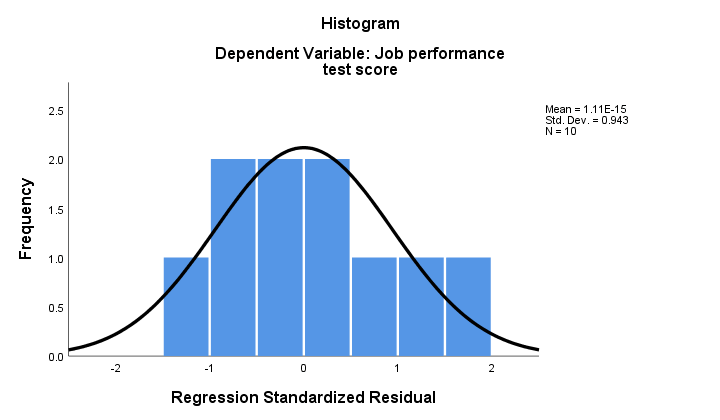
o procedimento de regressão pode adicionar esses resíduos como uma nova variável aos seus dados. Ao fazer isso, você poderia executar um teste Kolmogorov-Smirnov para normalidade sobre eles. Para a pequena amostra em mãos, no entanto, este teste dificilmente terá qualquer poder estatístico. Então, vamos pular.

o 3. linearidade e 4. as suposições de homocedasticidade são melhor avaliadas a partir de um gráfico residual. Este é um gráfico de dispersão com valores previstos no eixo x e resíduos no eixo y, conforme mostrado abaixo. Ambas as variáveis foram padronizadas, mas isso não afeta a forma do padrão de pontos.

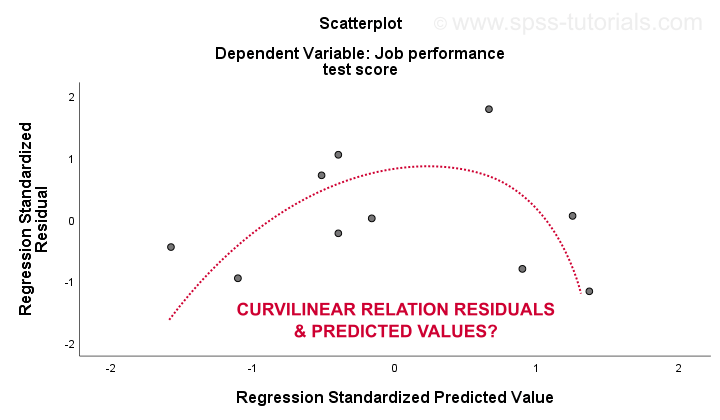
honestamente, o gráfico residual mostra forte curvilinearidade. Desenhei manualmente a curva que acho que se encaixa melhor no padrão geral. Assumir uma relação curvilínea provavelmente resolve a heteroscedasticidade também, mas as coisas estão ficando muito técnicas agora.O ponto básico é simplesmente que algumas suposições não são válidas.As soluções mais comuns para estes problemas -do pior para o melhor – são

• ignorar esses pressupostos completamente;
• mentir que a regressão parcelas não indicam quaisquer violações do modelo de pressupostos;
• uma transformação não-linear -como logarítmica para a variável dependente;
• montagem de uma curvilínea modelo -que a gente vai dar um tiro em um minuto.

Diretrizes APA para relatar Regressão

a figura abaixo é-literalmente – uma ilustração de livro didático para relatar regressão no formato APA.

criar esta tabela exata a partir da saída do SPSS é uma dor real na Bunda. Editá-lo é mais fácil no Excel do que no WORD, para que você possa economizar pelo menos alguns problemas.
alternativamente, tente fugir com copy-colando a saída SPSS (não editada) e finja não estar ciente do formato APA exato.

experiência de regressão não Linear

Nosso tamanho de amostra é muito pequeno para realmente caber qualquer coisa além de um modelo linear. Mas fizemos isso de qualquer maneira-apenas curiosidade. A opção mais fácil no SPSS está em analisar Regressão estimativa da curva.Não vamos discutir os diálogos, mas colamos a sintaxe abaixo.

sintaxe de regressão não Linear SPSS

resultados

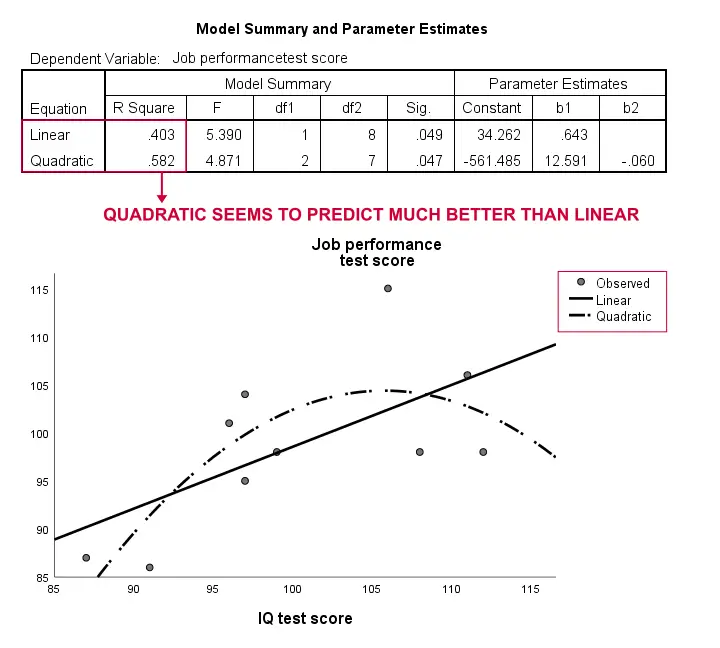
novamente, Nossa amostra é muito pequena para concluir qualquer coisa séria. No entanto, os resultados sugerem que um modelo Curvilíneo se encaixa muito melhor em nossos dados do que o linear. Não vamos explorar mais isso, mas queríamos mencioná-lo; sentimos que os modelos curvilíneos são rotineiramente negligenciados por cientistas sociais.

obrigado pela leitura!