como encontrar derivativos de Alta Ordem
encontrar uma segunda, terceira, quarta ou maior derivada é incrivelmente simples. A segunda derivada de uma função é apenas a derivada de sua primeira derivada. A terceira derivada é a derivada da segunda derivada, a quarta derivada é a derivada da terceira e assim por diante.
por exemplo, aqui está uma função e sua primeira, segunda, terceira e derivadas subsequentes. Neste exemplo, todos os derivados são obtidos pela regra de poder:
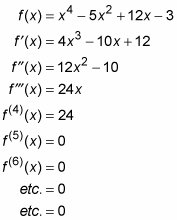
todas as funções polinomiais como esta eventualmente vão para zero quando você se diferencia repetidamente. Por outro lado, funções racionais, como
obter messier e messier como você tomar mais e mais derivados. E os derivados mais altos do seno e do cosseno são cíclicos. Por exemplo,
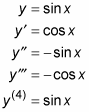
O ciclo se repete indefinidamente com cada múltiplo de quatro.
uma primeira derivada informa a rapidez com que uma função está mudando — a rapidez com que ela está subindo ou descendo — essa é sua inclinação. Uma segunda derivada informa a rapidez com que a primeira derivada está mudando — ou, em outras palavras, a rapidez com que a inclinação está mudando. Uma terceira derivada informa a rapidez com que a segunda derivada está mudando, o que informa a rapidez com que a taxa de mudança da inclinação está mudando.
se você está ficando um pouco perdido aqui, não se preocupe com isso. Fica cada vez mais difícil entender o que os derivados mais altos lhe dizem à medida que você passa pela segunda derivada, porque você começa a entrar em uma taxa de mudança de uma taxa de mudança de uma taxa de mudança e assim por diante.




