SPSS prosta regresja liniowa Tutorial
- Utwórz punkt rozproszony za pomocą Fit Line
- okna dialogowe regresji liniowej SPSS
- interpretacja wyników regresji SPSS
- ocena założeń regresji
- wytyczne APA dotyczące raportowania regresji
Pytanie badawcze i dane
firma X miała 10 pracowników, którzy przeszli test IQ i wydajności pracy. Uzyskane dane-część z nich są pokazane poniżej – są w prostej-liniowej-regresji.sav.
najważniejsze firma X chce dowiedzieć się, czy IQ przewiduje wydajność pracy? A jeśli tak, to jak?Odpowiemy na te pytania, przeprowadzając prostą analizę regresji liniowej w SPSS.
Utwórz punkt rozproszenia za pomocą Fit Line
świetnym punktem wyjścia do naszej analizy jest punkt rozproszenia. To nam powie, czy wyniki IQ i performance oraz ich związek-jeśli w ogóle-mają jakikolwiek sens. Stworzymy nasz Wykres z Wykresów  starsze okna dialogowe
starsze okna dialogowe  Scatter/Dot, a następnie wykonamy poniższe zrzuty ekranu.
Scatter/Dot, a następnie wykonamy poniższe zrzuty ekranu.
 osobiście lubię wrzucać
osobiście lubię wrzucać
- tytuł, który mówi, na co w zasadzie patrzą moi odbiorcy i
- podtytuł, który mówi, którzy respondenci lub obserwacje są pokazywane i ilu.
przechodzenie przez okna dialogowe skutkowało poniższą składnią. Sprawdźmy to.
SPSS Scatterplot ze składnią tytułów
GRAPH
/SCATTERPLOT(BIVAR)=IQ z wydajnością
/MISSING=LISTWISE
/TITLE=’scatterplot z wydajnością
| subtitle’All respondents / N = 10′.
wynik
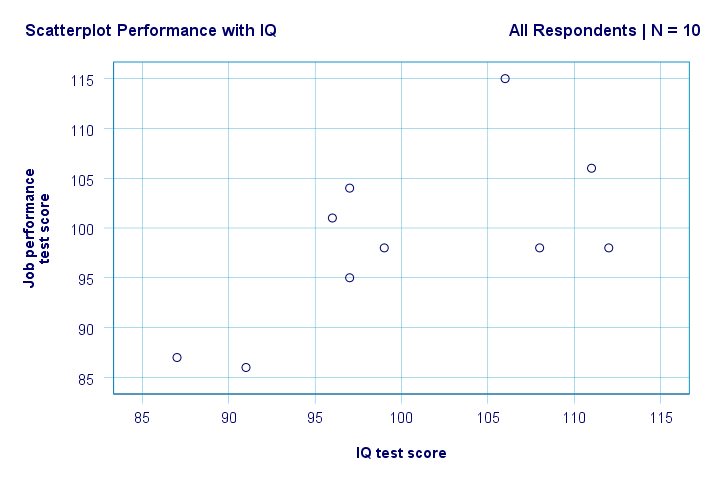
prawo. Więc po pierwsze, nie widzimy niczego dziwnego w naszym planie rozproszenia. Wydaje się, że istnieje umiarkowana korelacja między IQ a wydajnością: średnio respondenci z wyższym wynikiem IQ wydają się lepiej wykonywać. Ta relacja wygląda mniej więcej liniowo.
dodajmy teraz linię regresji do naszego punktu rozproszonego . Kliknięcie prawym przyciskiem myszy i wybranie Edytuj zawartość  w osobnym oknie otwiera okno edytora Wykresów. Tutaj po prostu klikamy ikonę „Dodaj linię dopasowania w sumie”, jak pokazano poniżej.
w osobnym oknie otwiera okno edytora Wykresów. Tutaj po prostu klikamy ikonę „Dodaj linię dopasowania w sumie”, jak pokazano poniżej.
domyślnie SPSS dodaje teraz linię regresji liniowej do naszej tabeli rozproszonej. Wynik pokazano poniżej.
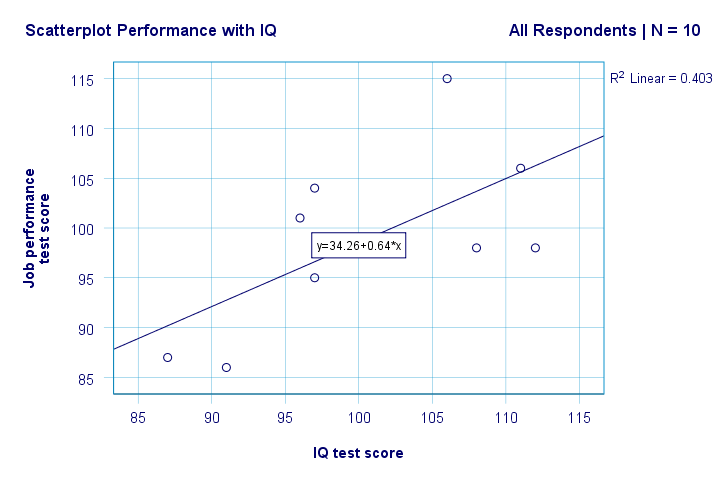
mamy teraz kilka pierwszych podstawowych odpowiedzi na nasze pytania badawcze. R2 = 0,403 wskazuje, że IQ stanowi około 40,3% wariancji w wynikach. Oznacza to, że IQ przewiduje wydajność dość dobrze w tej próbie.
ale jak najlepiej przewidzieć wyniki pracy z IQ? Cóż, w naszej tabeli punktowej y to wydajność (pokazana na osi y), a x to IQ (pokazane na osi x). Więc to będzie wynik = 34,26 + 0,64 * IQ.So dla kandydata z wynikiem IQ 115, przewidujemy 34.26 + 0.64 * 115 = 107.86 jako jego / jej najbardziej prawdopodobny wynik w przyszłości.
racja, więc daje nam to podstawowe pojęcie o relacji między IQ a wydajnością i przedstawia ją wizualnie. Jednak nadal brakuje wielu informacji-istotności statystycznej i przedziałów ufności. Więc chodźmy po niego.
okna dialogowe regresji liniowej SPSS
ponowne uruchomienie naszej minimalnej analizy regresji z analizy  regresja
regresja  liniowa daje nam znacznie bardziej szczegółowe wyniki. Poniższe zrzuty ekranu pokazują, jak będziemy postępować.
liniowa daje nam znacznie bardziej szczegółowe wyniki. Poniższe zrzuty ekranu pokazują, jak będziemy postępować.
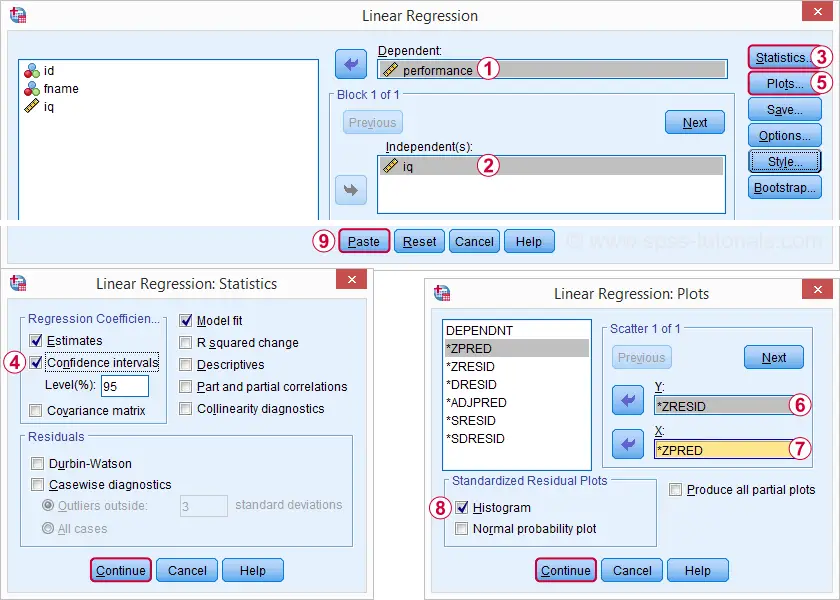
wybranie tych opcji skutkuje poniższą składnią. Sprawdźmy to.
SPSS prosta składnia regresji liniowej
REGRESJA
/ LISTA ZAGINIONYCH
/ STATYSTYKA KOEFF (95) R ANOVA
/CRITERIA=PIN (.05) POUT(.10)
/ NOORIGIN
/ DEPENDENT performance
/METHOD=ENTER iq
/SCATTERPLOT=(*ZERID ,*ZPRED)
/ RESIDUALS HISTOGRAM(ZERID).
wyjście regresji SPSS i – współczynniki
niestety, SPSS daje nam znacznie więcej wyjścia regresji niż potrzebujemy. Możemy bezpiecznie zignorować większość z nich. Jednak tabelą o dużym znaczeniu jest tabela współczynników przedstawiona poniżej.
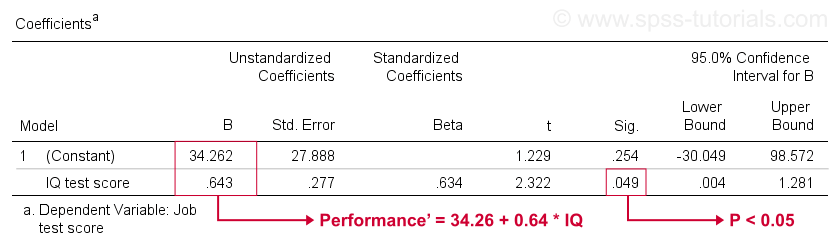
ta tabela pokazuje współczynniki B, które już widzieliśmy w naszym punkcie rozpraszania. Jak wskazano, implikują one równanie regresji liniowej, które najlepiej szacuje wydajność pracy z IQ w naszej próbie.
Po Drugie, pamiętaj, że zwykle odrzucamy hipotezę zerową, jeśli p < 0.05. Współczynnik B dla IQ ma „Sig” czyli p = 0,049. Statystycznie znacząco różni się od zera.
jednak jego 95% przedział ufności-z grubsza prawdopodobny przedział dla jego wartości populacji-jest . Więc B prawdopodobnie nie jest zerem, ale może być bardzo blisko zera. Przedział ufności jest ogromny – nasze oszacowanie dla B nie jest w ogóle precyzyjne – a wynika to z minimalnej wielkości próbki, na której opiera się analiza.
wyjście regresji SPSS II – podsumowanie modelu
oprócz tabeli współczynników, potrzebujemy również tabeli podsumowania modelu do raportowania naszych wyników.
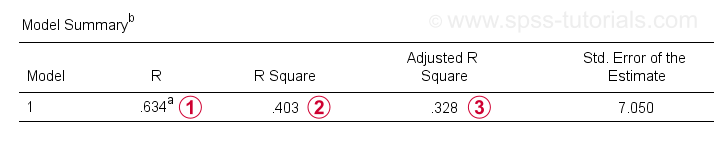
 R jest korelacją między przewidywanymi wartościami regresji a wartościami rzeczywistymi. Dla regresji prostej R jest równy korelacji między predyktorem a zmienną zależną.
R jest korelacją między przewidywanymi wartościami regresji a wartościami rzeczywistymi. Dla regresji prostej R jest równy korelacji między predyktorem a zmienną zależną.
 R kwadrat-korelacja kwadratowa-wskazuje proporcję wariancji w zmiennej zależnej, która jest rozliczana przez predyktor(y) w naszych próbkach danych.
R kwadrat-korelacja kwadratowa-wskazuje proporcję wariancji w zmiennej zależnej, która jest rozliczana przez predyktor(y) w naszych próbkach danych.
 skorygowane szacunki R-kwadrat R-kwadrat przy zastosowaniu naszego równania regresji (na podstawie próbki) do całej populacji.
skorygowane szacunki R-kwadrat R-kwadrat przy zastosowaniu naszego równania regresji (na podstawie próbki) do całej populacji.
skorygowany r-kwadrat daje bardziej realistyczne oszacowanie dokładności predykcyjnej niż po prostu R-kwadrat. W naszym przykładzie duża różnica między nimi-ogólnie określana jako skurcz – wynika z naszego bardzo minimalnego rozmiaru próbki tylko N = 10.
w każdym razie jest to zła wiadomość dla firmy X: IQ w końcu tak ładnie nie przewiduje wyników pracy.
ocena założeń regresji
głównymi założeniami regresji są
- niezależne obserwacje;
- normalność: błędy muszą następować po normalnym rozkładzie w populacji;
- Liniowość: zależność między każdym predyktorem a zmienną zależną jest liniowa;
- Homoscedastyczność: błędy muszą mieć stałą wariancję na wszystkich poziomach przewidywanej wartości.
1. Jeśli każdy przypadek (rząd komórek w widoku danych) w SPSS reprezentuje oddzielną osobę, zwykle Zakładamy, że są to „niezależne obserwacje”. Następnie założenia 2-4 są najlepiej oceniane przez kontrolę Wykresów regresji w naszym wyjściu.
2. Jeśli normalność utrzymuje się, to nasze pozostałości regresji powinny być (z grubsza) normalnie rozłożone. Poniższy histogram nie pokazuje wyraźnego odejścia od normalności.
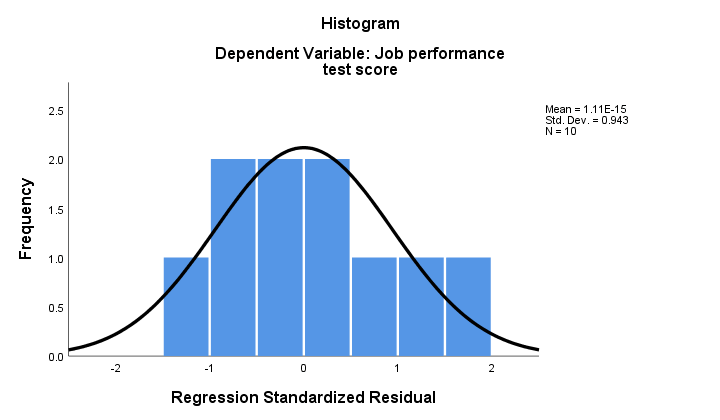
procedura regresji może dodać te pozostałości jako nową zmienną do danych. W ten sposób możesz przeprowadzić na nich test Kołmogorowa-Smirnowa na normalność. Jednak w przypadku niewielkiej próbki test ten nie będzie miał żadnej mocy statystycznej. Pomińmy to.
3. liniowość i 4. założenia homoscedastyczności najlepiej oceniać na podstawie wykresu szczątkowego. Jest to punkt rozproszony z przewidywanymi wartościami w osi x i pozostałościami na osi y, jak pokazano poniżej. Obie zmienne zostały znormalizowane, ale nie wpływa to na kształt wzoru kropek.
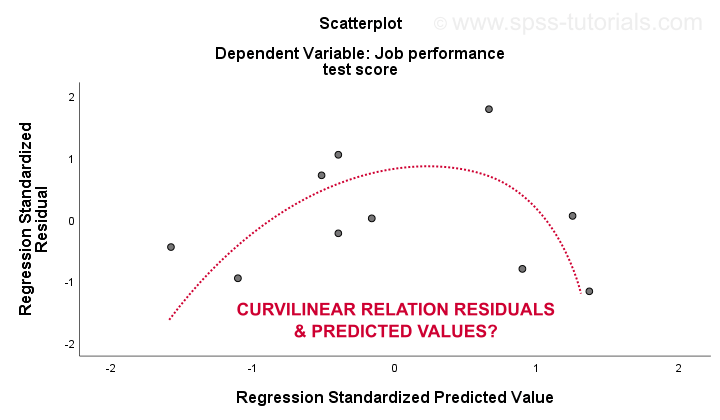
szczerze mówiąc, Wykres resztkowy wykazuje silną krzywizność. Ręcznie narysowałem krzywą, która moim zdaniem najlepiej pasuje do ogólnego wzoru. Zakładając, że krzywoliniowa relacja prawdopodobnie rozwiązuje również heteroscedastyczność, ale teraz sprawy stają się zbyt techniczne.Podstawową kwestią jest po prostu to, że niektóre założenia się nie trzymają.Najczęstsze rozwiązania tych problemów – od najgorszych do najlepszych-to
- całkowicie ignorując te założenia;
- leżąc, że wykresy regresji nie wskazują na jakiekolwiek naruszenia założeń modelu;
- nieliniowe przekształcenie-takie jak logarytmiczne – do zmiennej zależnej;
- dopasowanie modelu krzywoliniowego-który damy strzał za minutę.
wytyczne APA dotyczące raportowania regresji
poniższy rysunek jest-całkiem dosłownie – podręcznikową ilustracją do raportowania regresji w formacie APA.

Tworzenie tej dokładnej tabeli z wyników SPSS jest prawdziwym wrzodem na tyłku. Edycja jest łatwiejsza w programie Excel niż w programie WORD, dzięki czemu możesz zaoszczędzić co najmniej kłopotów.
alternatywnie, spróbuj uciec od kopiowania-wklejania (nieedytowanego) wyjścia SPSS i udawaj, że nie jesteś świadomy dokładnego formatu APA.
eksperyment regresji nieliniowej
Nasz rozmiar próbki jest zbyt mały, aby naprawdę zmieścić coś poza modelem liniowym. Ale i tak to zrobiliśmy-po prostu ciekawość. Najprostszą opcją w SPSS jest analiza regresja
regresja Szacowanie krzywej.Nie będziemy omawiać dialogów, ale wkleiliśmy składnię poniżej.
Szacowanie krzywej.Nie będziemy omawiać dialogów, ale wkleiliśmy składnię poniżej.
SPSS składnia regresji nieliniowej
TSET NEWVAR=NONE.
CURVEFIT
/ VARIABLES= performance WITH iq
/CONSTANT
/MODEL = quadratic linear
/PLOT FIT.
wyniki
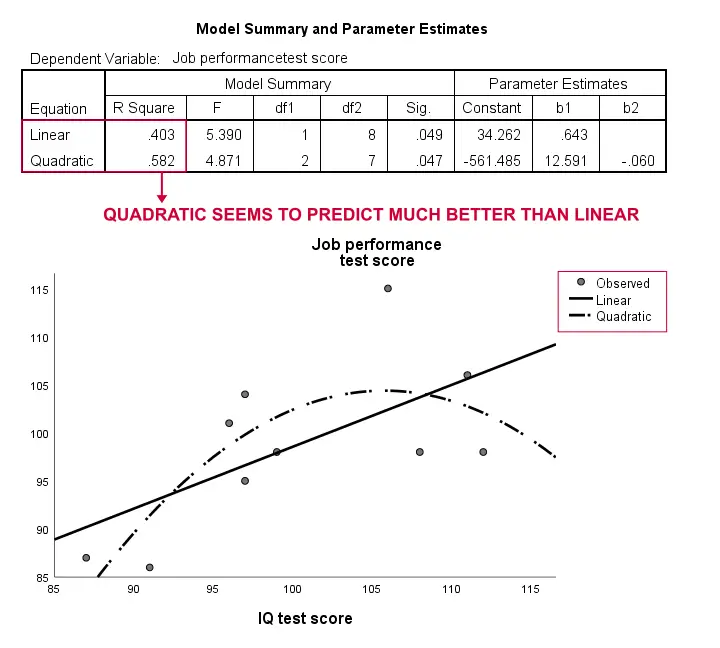
ponownie, nasza próba jest zbyt mała, aby stwierdzić coś poważnego. Jednak wyniki sugerują, że model krzywoliniowy pasuje do naszych danych znacznie lepiej niż liniowy. Nie będziemy badać tego dalej, ale chcieliśmy o tym wspomnieć; czujemy, że modele krzywoliniowe są rutynowo pomijane przez naukowców społecznych.
dzięki za przeczytanie!




