SPSS Simple Linear Regression Tutorial

SPSS Simple Linear Regression Tutorial

1. Creëer een Scatterplot met Fit Line
2. SPSS Linear Regression Dialogs
3. interpreteren van SPSS Regression Output
4. evalueren van de Regressieaannames
5. Apa Guidelines for Reporting Regression

onderzoeksvraag en-gegevens

bedrijf X had 10 werknemers doe een IQ en job performance test. De resulterende gegevens-waarvan een deel hieronder wordt weergegeven-zijn in eenvoudige-lineaire-regressie.sav.

het belangrijkste ding bedrijf X wil achterhalen isdoes IQ voorspellen job performance? En zo ja, hoe?We zullen deze vragen beantwoorden door een eenvoudige lineaire regressieanalyse uit te voeren in SPSS.

Scatterplot aanmaken met Fit Line

een goed uitgangspunt voor onze Analyse is een scatterplot. Dit zal ons vertellen of het IQ en de prestaties scores en hun relatie-indien van toepassing – zinvol in de eerste plaats. We maken onze grafiek van grafieken Legacy dialogen Scatter / Dot en we volgen de screenshots hieronder.

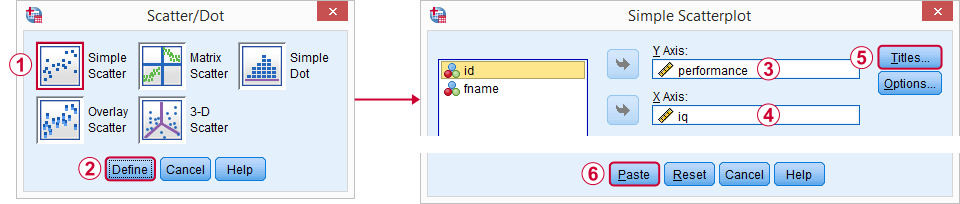
• een titel die zegt waar mijn publiek naar kijkt en
• een ondertitel die zegt welke respondenten of observaties worden getoond en hoeveel.

lopen door de dialogen resulteerde in de syntaxis hieronder. Dus laten we het controleren.

SPSS verstrooien met titels syntaxis

resultaat

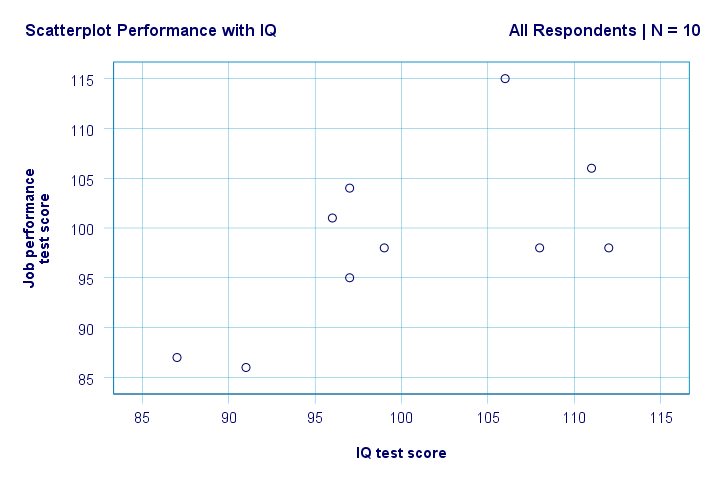
rechts. Dus ten eerste zien we niets raars in onze scatterplot. Er lijkt een matige correlatie te zijn tussen IQ en prestaties: gemiddeld lijken respondenten met hogere IQ-scores beter te presteren. Deze relatie ziet er ruwweg lineair uit.
laten we nu een regressielijn toevoegen aan ons scatterplot. Klik er met de rechtermuisknop op en selecteer Inhoud bewerken in een apart venster opent een grafiekbewerker venster. Hier klikken we gewoon op de “voeg Fit lijn bij Totaal” icoon zoals hieronder getoond.

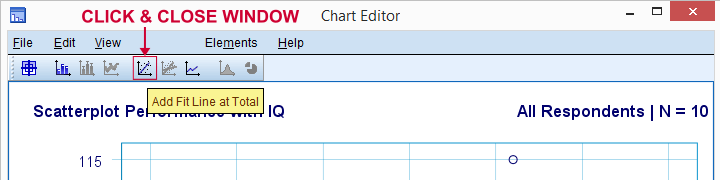
standaard voegt SPSS nu een lineaire regressielijn toe aan ons scatterplot. Het resultaat wordt hieronder weergegeven.

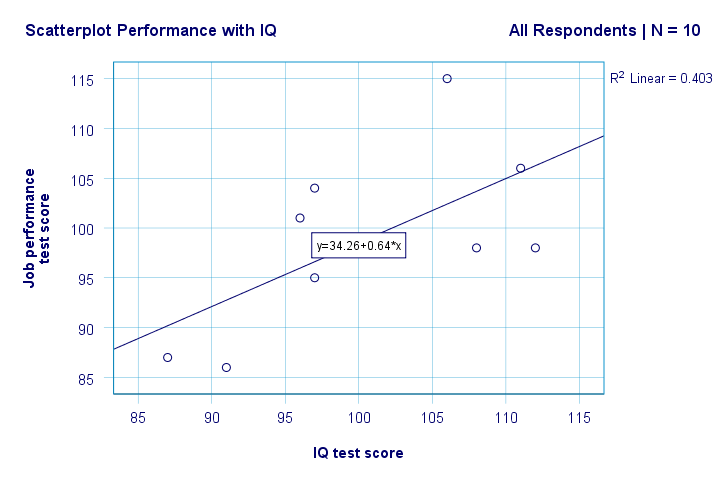
we hebben nu enkele eerste fundamentele antwoorden op onze onderzoeksvragen. R2 = 0,403 geeft aan dat IQ goed is voor ongeveer 40,3% van de variantie in prestatiescores. Dat wil zeggen, IQ voorspelt de prestaties vrij goed in deze steekproef.
maar hoe kunnen we de prestaties van IQ het best voorspellen? Nou, in ons scatterplot y is performance (getoond op de y-as) en x is IQ (getoond op de x-as). Dus dat zal zijnperformance = 34,26 + 0,64 * IQ.So voor een sollicitant met een IQ score van 115, zullen we voorspellen 34.26 + 0.64 * 115 = 107.86 als zijn / haar meest waarschijnlijke toekomstige Prestatiescore.
rechts, dus dat geeft ons een basisidee over de relatie tussen IQ en prestaties en geeft het visueel weer. Er ontbreekt echter nog veel informatie-statistische significantie en betrouwbaarheidsintervallen -. Dus laten we het gaan halen.

SPSS-Lineaire Regressiedialogen

het opnieuw uitvoeren van onze minimale regressieanalyse uit analyse regressie lineair geeft ons veel meer gedetailleerde uitvoer. De screenshots hieronder laten zien hoe we verder gaan.

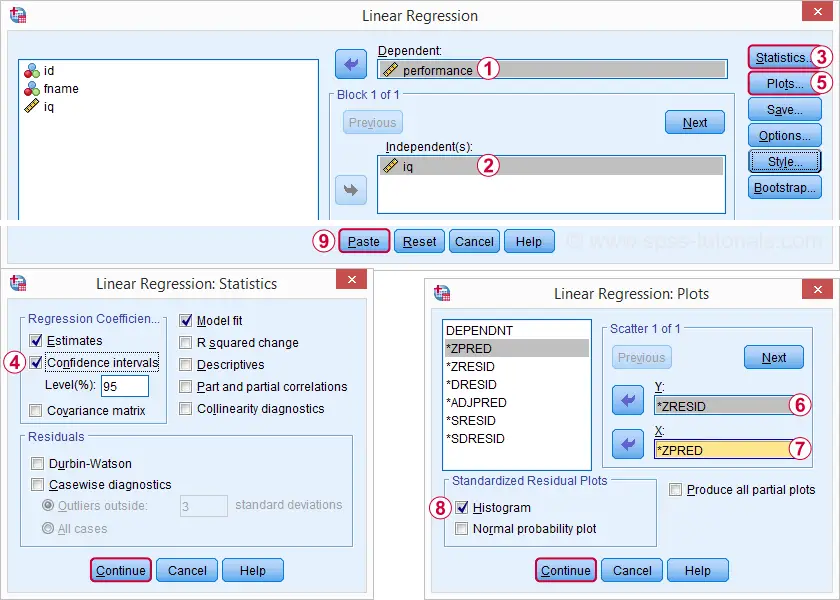
het selecteren van deze opties resulteert in de syntaxis hieronder. Laten we het natrekken.

SPSS eenvoudige lineaire regressie syntaxis

SPSS Regressieoutput I-coëfficiënten

helaas geeft SPSS ons veel meer regressieoutput dan we nodig hebben. We kunnen het meeste veilig negeren. Echter, een tabel van groot belang is de coëfficiënten tabel hieronder weergegeven.

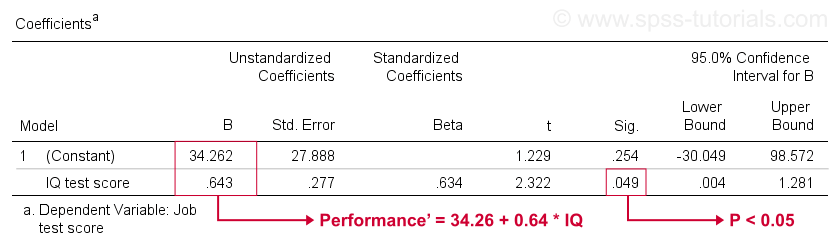
deze tabel toont de B-coëfficiënten die we al zagen in ons verstrooiingsschema. Zoals aangegeven, impliceren deze de lineaire regressievergelijking die de beste schatting job performance van IQ in onze steekproef.Ten tweede, onthoud dat we meestal de nulhypothese afwijzen als p < 0,05. De B-coëfficiënt voor IQ heeft ” Sig ” of p = 0,049. Het is statistisch significant verschillend van nul.
echter, het 95% betrouwbaarheidsinterval-ruwweg een waarschijnlijk bereik voor de populatiewaarde – is . Dus B is waarschijnlijk niet nul, maar het kan heel goed dicht bij nul zijn. Het betrouwbaarheidsinterval is enorm-onze schatting voor B is helemaal niet precies-en dit is te wijten aan de minimale steekproefgrootte waarop de analyse is gebaseerd.

SPSS regressie Output II-Model Summary

naast de coëfficiëntentabel hebben we ook de Model Summary table nodig voor het rapporteren van onze resultaten.

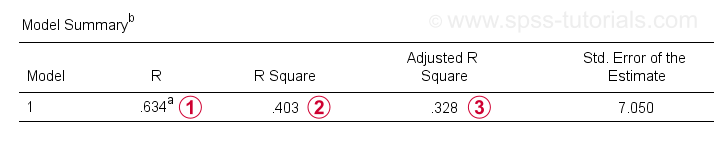
R is de correlatie tussen de voorspelde regressiewaarden en de werkelijke waarden. Voor eenvoudige regressie is R gelijk aan de correlatie tussen de voorspeller en de afhankelijke variabele.
R kwadraat-de kwadraatcorrelatie-geeft de variantieverhouding in de afhankelijke variabele aan die wordt verklaard door de voorspeller(s) in onze steekproefgegevens.
aangepaste R-kwadraatschattingen R-kwadraat bij toepassing van onze (op steekproef gebaseerde) regressievergelijking op de gehele populatie.
aangepast R-kwadraat geeft een realistischer schatting van de voorspellende nauwkeurigheid dan gewoon r-kwadraat. In ons voorbeeld is het grote verschil tussen hen-meestal aangeduid als krimp – te wijten aan onze zeer minimale steekproefgrootte van slechts n = 10.
in ieder geval is dit slecht nieuws voor bedrijf X: IQ voorspelt toch niet zo goed de prestaties van de baan.

evaluatie van de aannames voor regressie

de belangrijkste aannames voor regressie zijn

1. onafhankelijke waarnemingen;
2. normaliteit: fouten moeten een normale verdeling in de populatie volgen;
3. lineariteit: de relatie tussen elke voorspeller en de afhankelijke variabele is lineair;
4. Homoscedasticiteit: fouten moeten een constante variantie hebben over alle niveaus van de voorspelde waarde.

1. Als elk geval (rij cellen in gegevensweergave) in SPSS een afzonderlijke persoon vertegenwoordigt, gaan we er meestal van uit dat dit “onafhankelijke waarnemingen”zijn. Vervolgens worden aannames 2-4 het best geëvalueerd door de regressiepercelen in onze output te inspecteren.

2. Als normaliteit geldt, dan moeten onze regressieresten (ruwweg) normaal worden verdeeld. Het histogram hieronder laat geen duidelijke afwijking van de normaliteit zien.

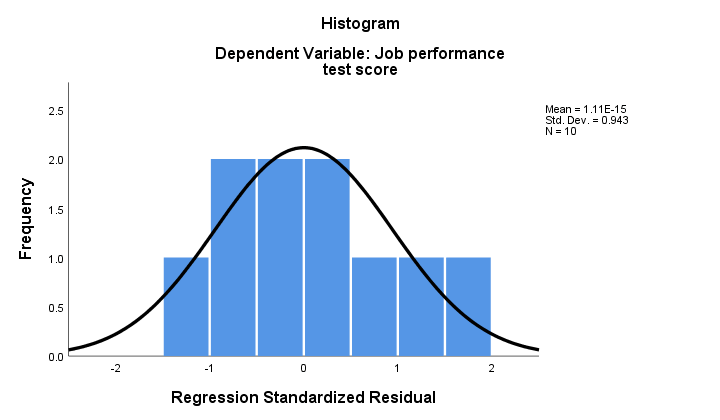
de regressieprocedure kan deze reststoffen als een nieuwe variabele aan uw gegevens toevoegen. Door dit te doen, kunt u een Kolmogorov-Smirnov test voor normaliteit op hen uitvoeren. Voor het kleine monster bij de hand zal deze test echter nauwelijks statistische kracht hebben. Dus laten we het overslaan.

de 3. lineariteit en 4. homoscedasticiteit veronderstellingen worden het best beoordeeld op basis van een restperceel. Dit is een scatterplot met voorspelde waarden in de x-as en reststoffen op de y-as zoals hieronder weergegeven. Beide variabelen zijn gestandaardiseerd maar dit heeft geen invloed op de vorm van het patroon van punten.

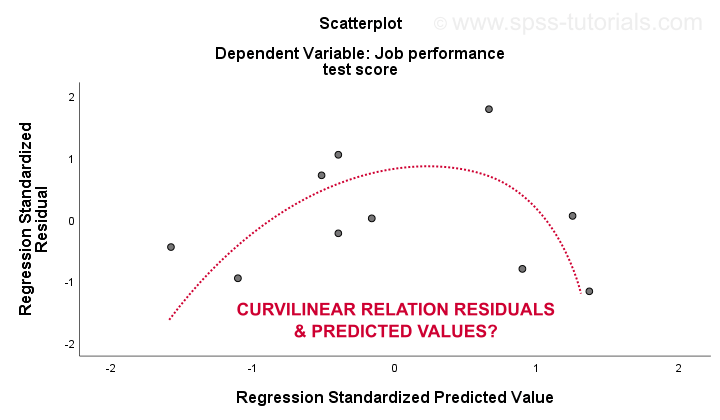
eerlijk gezegd vertoont het resterende plot een sterke kromlijnigheid. Ik tekende handmatig de curve die ik denk dat het beste past bij het algemene patroon. Het aannemen van een kromlijnige relatie lost waarschijnlijk ook de heteroscedasticiteit op, maar de dingen worden nu veel te technisch.Het fundamentele punt is gewoon dat sommige veronderstellingen niet kloppen.De meest voorkomende oplossingen voor deze problemen – van het slechtste naar het beste-zijn

• deze aannames totaal negeren;
• liegen dat de regressiegrafieken geen schendingen van de modelaannames aangeven;
• een niet-lineaire transformatie – zoals logaritmisch – naar de afhankelijke variabele;
• passen van een kromlijnig model-dat we in een minuut een kans geven.

Apa Guidelines for Reporting Regression

onderstaande figuur is-letterlijk-een tekstboekillustratie voor het rapporteren van regressie in APA-formaat.

het creëren van deze exacte tabel uit de SPSS output is een echte pijn in de kont. Bewerken gaat gemakkelijker in Excel dan in WORD, zodat u op zijn minst wat problemen kunt besparen.
u kunt ook proberen weg te komen met het kopiëren van de (onbewerkte) SPSS-uitvoer en doen alsof u zich niet bewust bent van het exacte APA-formaat.

Non Linear Regression Experiment

onze steekproefgrootte is te klein om echt iets te passen buiten een lineair model. Maar we deden het toch-gewoon nieuwsgierigheid. De eenvoudigste optie in SPSS is onder analyseer regressie Curve schatting.We zijn niet van plan om de dialogen te bespreken, maar we hebben de syntaxis hieronder geplakt.

SPSS niet-lineaire regressie syntaxis

resultaten

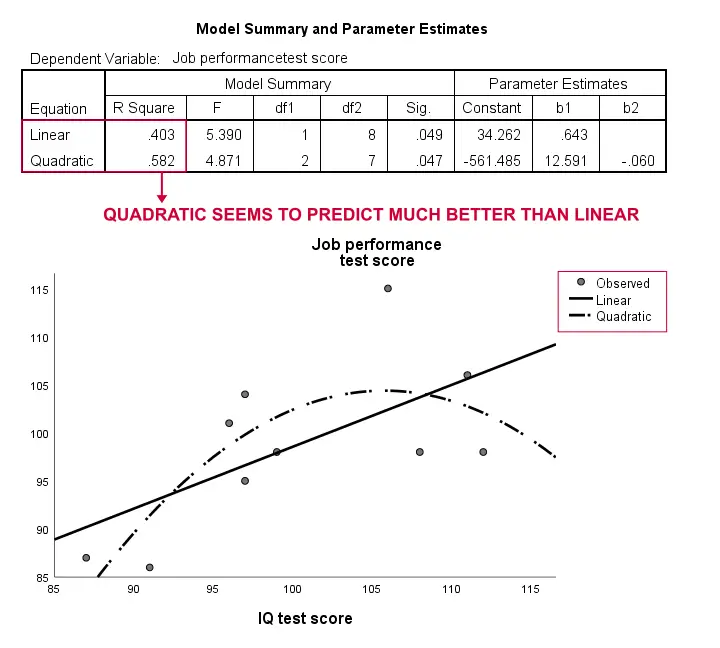
nogmaals, onze steekproef is veel te klein om iets ernstigs te concluderen. Echter, de resultaten doen een beetje suggereren dat een kromlijnig model past onze gegevens veel beter dan de lineaire. We zullen dit niet verder onderzoeken, maar we wilden het wel vermelden; we vinden dat kromlijnige modellen routinematig over het hoofd worden gezien door sociale wetenschappers.

Bedankt voor het lezen!