Hoe vind je High-Order derivaten
het vinden van een tweede, derde, vierde of hogere afgeleide is ongelooflijk eenvoudig. De tweede afgeleide van een functie is slechts de afgeleide van zijn eerste afgeleide. De derde afgeleide is de afgeleide van de tweede afgeleide, de vierde afgeleide is de afgeleide van de derde, enzovoort.
bijvoorbeeld, hier is een functie en zijn eerste, tweede, derde en volgende derivaten. In dit voorbeeld worden alle derivaten verkregen door de macht regel:
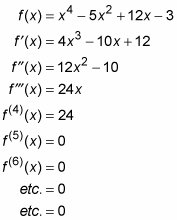
alle veeltermfuncties zoals deze gaan uiteindelijk naar nul als je herhaaldelijk differentieert. Aan de andere kant, rationele functies zoals
krijg messier en messier als je hogere en hogere derivaten te nemen. En de hogere derivaten van sinus en cosinus zijn cyclisch. Bijvoorbeeld:,
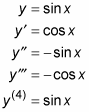
de cyclus herhaalt zich oneindig met elk veelvoud van vier.
een eerste afgeleide vertelt je hoe snel een functie verandert – hoe snel hij omhoog of omlaag gaat-dat is zijn helling. Een tweede afgeleide vertelt je hoe snel de eerste afgeleide verandert — of, met andere woorden, hoe snel de helling verandert. Een derde afgeleide vertelt je hoe snel de tweede afgeleide verandert, wat je vertelt hoe snel de snelheid van verandering van de helling verandert.
als je hier een beetje verdwaald raakt, maak je er geen zorgen over. Het wordt steeds moeilijker om een greep te krijgen op wat hogere derivaten je vertellen als je voorbij de tweede afgeleide gaat, omdat je in een snelheid van verandering van een snelheid van verandering van een snelheid van verandering begint te komen, enzovoort.




