SPSS Enkel Lineær Regresjon Tutorial

SPSS Enkel Lineær Regresjon Tutorial

1. Lag Scatterplot Med Fit Line
2. Spss Lineær Regresjon Dialoger
3. Tolke SPSS Regresjon Utgang
4. Evaluere Regresjon Forutsetninger
5. TFO Retningslinjer For Rapportering Regresjon

Forskningsspørsmål og Data

Firma X Hadde 10 Ansatte Ta En Iq Og Jobbprestasjonstest. De resulterende dataene-hvorav en del er vist nedenfor – er i enkel-lineær regresjon.sav.

det viktigste Selskapet X ønsker å finne ut erspår IQ jobbprestasjon? Og-i så fall-hvordan?Vi svarer på disse spørsmålene ved å kjøre en enkel lineær regresjonsanalyse i SPSS.

Lag Scatterplot Med Fit Line

et flott utgangspunkt for vår analyse er en scatterplot. Dette vil fortelle oss om IQ og ytelse score og deres forhold-hvis noen-gi noen mening i første omgang. Vi lager diagrammet vårt fra Grafer Eldre Dialoger Scatter / Dot, og vi følger deretter skjermbildene nedenfor.

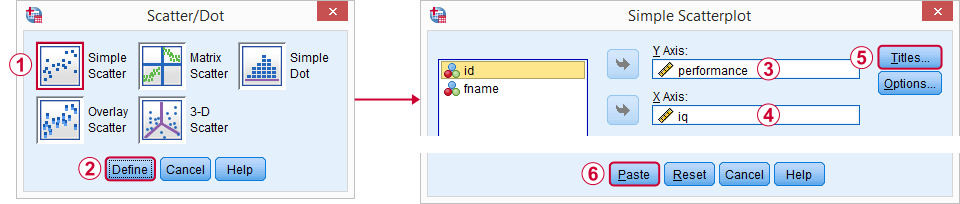
jeg personlig liker å kaste inn

• en tittel som sier hva publikum i utgangspunktet ser på og
• en undertekst som sier hvilke respondenter eller observasjoner som vises og hvor mange.

Å Gå gjennom dialogene resulterte i syntaksen nedenfor. Så la oss kjøre den.

SPSS Scatterplot Med Titler Syntaks

Resultat

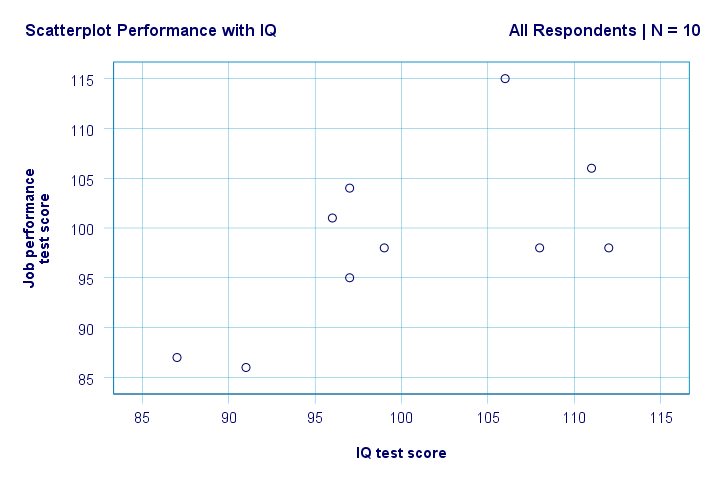
Høyre. Så først ser vi ikke noe rart i vår scatterplot. Det synes å være en moderat sammenheng MELLOM IQ og ytelse: i gjennomsnitt ser respondenter med høyere IQ-poeng ut til å fungere bedre. Dette forholdet ser omtrent lineært ut.
La oss nå legge til en regresjonslinje til vår scatterplot. Høyreklikk på det og velg Rediger innhold i Eget Vindu åpnes Et Diagramredigeringsvindu. Her klikker vi bare på» Add Fit Line At Total » – ikonet som vist nedenfor.

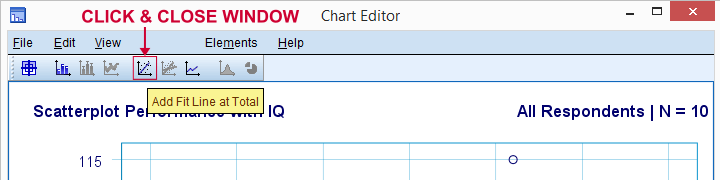
SOM standard legger SPSS nå en lineær regresjonslinje til vår scatterplot. Resultatet er vist nedenfor.

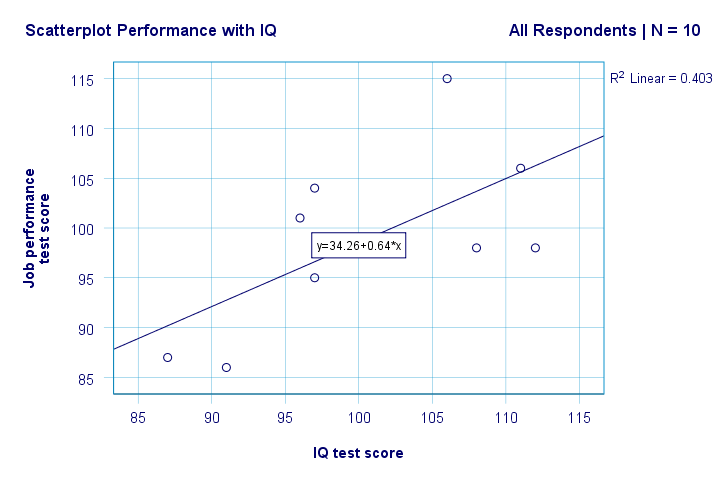
Vi har nå noen første grunnleggende svar på våre forskningsspørsmål. R2 = 0,403 indikerer AT IQ står for rundt 40,3% av variansen i resultatpoeng. DET vil SI AT IQ forutser ytelsen ganske bra i denne prøven.
men hvordan kan VI best forutsi jobbprestasjon fra IQ? Vel, i vår scatterplot er y ytelse (vist på y-aksen) og x ER IQ (vist på x-aksen). Så det vil beperformance = 34.26 + 0.64 * IQ.So for en jobbsøker med EN IQ score på 115, vil vi forutsi 34.26 + 0.64 * 115 = 107.86 som hans / hennes mest sannsynlige fremtidige resultatscore.
Riktig, Så det gir oss en grunnleggende ide om forholdet MELLOM IQ og ytelse og presenterer det visuelt. Imidlertid mangler mye informasjon-statistisk signifikans og konfidensintervall – fortsatt. Så la oss gå og hente den.

Spss Lineære Regresjonsdialoger

Kjør vår minimale regresjonsanalyse fra Analyser Regresjon Lineær gir oss mye mer detaljert utdata. Skjermbildene nedenfor viser hvordan vi skal fortsette.

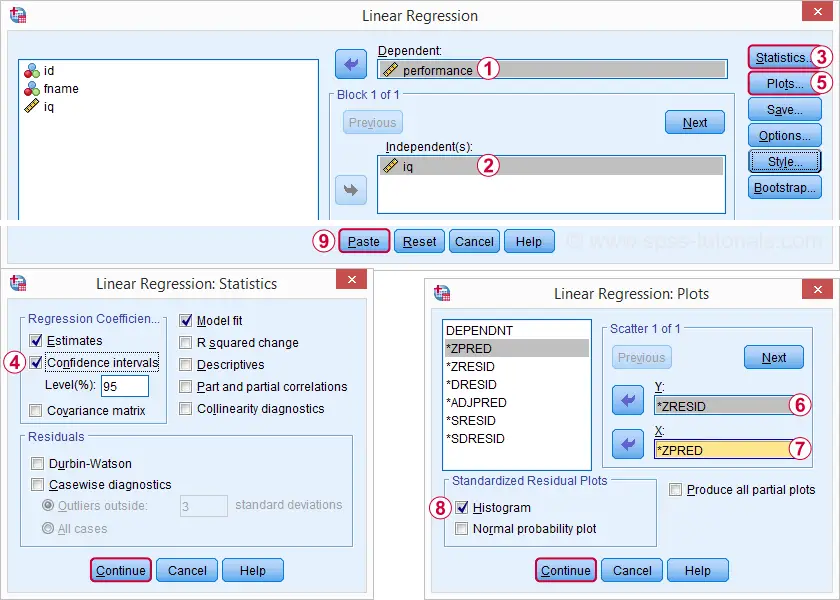
Valg av disse alternativene resulterer i syntaksen nedenfor. La oss kjøre den.

SPSS Enkel Lineær Regresjon Syntaks

SPSS Regresjonsutgang I – Koeffisienter

Dessverre gir SPSS oss mye mer regresjonsutgang enn vi trenger. Vi kan trygt ignorere det meste av det. Imidlertid er en tabell av stor betydning koeffisienttabellen vist nedenfor.

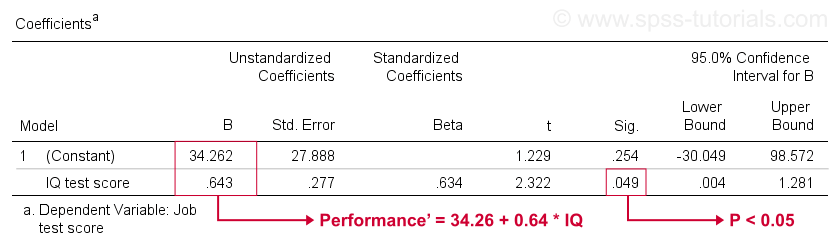
denne tabellen viser b-koeffisientene vi allerede så i vår scatterplot. Som angitt, innebærer disse den lineære regresjonsligningen som best anslår jobbytelse FRA IQ i vårt utvalg.
For Det Andre, husk at vi vanligvis avviser nullhypotesen hvis p < 0,05. B-koeffisienten FOR IQ har «Sig» eller p = 0,049. Det er statistisk signifikant forskjellig fra null.
imidlertid er 95% konfidensintervall-omtrent et sannsynlig område for befolkningsverdien -. Så B er sannsynligvis ikke null, men det kan vel være svært nær null. Konfidensintervallet er stort-vårt estimat For B er ikke presist i det hele tatt-og dette skyldes den minimale prøvestørrelsen som analysen er basert på.

SPSS Regresjon Utgang II-Modellsammendrag

Bortsett fra koeffisienttabellen, trenger Vi Også Modellsammendragstabellen for å rapportere resultatene våre.

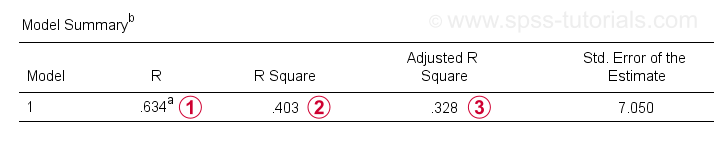
R er korrelasjonen mellom regresjonsverdiene og de faktiske verdiene. For enkel regresjon er R lik korrelasjonen mellom prediktor og avhengig variabel.
R Square-den kvadrerte korrelasjonen – angir andelen av variansen i den avhengige variabelen som regnskapsføres av prediktoren(e) i våre utvalgsdata.
Justerte r-kvadratestimater R-kvadrat ved bruk av vår (utvalgsbaserte) regresjonsligning til hele populasjonen.
Justert r-kvadrat gir et mer realistisk estimat av prediktiv nøyaktighet enn bare r-kvadrat. I vårt eksempel er den store forskjellen mellom dem-vanligvis referert til som krymping – på grunn av vår svært minimale prøvestørrelse På Bare N = 10.
I alle fall er dette dårlige nyheter FOR Firma X: IQ forutser egentlig ikke jobbprestasjon så pent.

Evaluering Av Regresjonsforutsetningene

hovedforutsetningene for regresjon er

1. Uavhengige observasjoner;
2. Normalitet: feil må følge en normalfordeling i populasjonen;
3. Linearitet: forholdet mellom hver prediktor og den avhengige variabelen er lineær;
4. Homoskedastisitet: feil må ha konstant varians over alle nivåer av spådd verdi.

1. Hvis hver sak (rad med celler i datavisning) i SPSS representerer en egen person, antar vi vanligvis at disse er «uavhengige observasjoner». Deretter vurderes antagelser 2-4 best ved å inspisere regresjonsplottene i produksjonen vår.

2. Hvis normalitet holder, bør våre regresjonsrester være (omtrent) normalfordelt. Histogrammet nedenfor viser ikke et klart avvik fra normalitet.

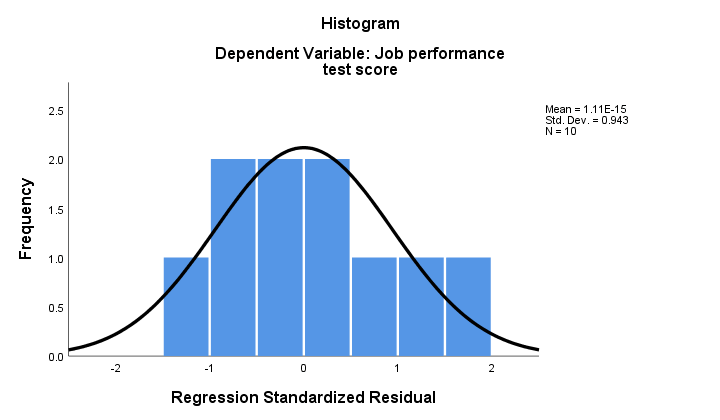
regresjonsprosedyren kan legge til disse residualene som en ny variabel i dataene dine. Ved å gjøre det, kan du kjøre En Kolmogorov-Smirnov test for normalitet på dem. For den lille prøven ved hånden vil imidlertid denne testen nesten ikke ha noen statistisk kraft. Så la oss hoppe over det.

Den 3. linearitet og 4. homoscedasticity antagelser er best evaluert fra en gjenværende tomt. Dette er en scatterplot med forventede verdier i x-aksen og residuals på y-aksen som vist nedenfor. Begge variablene er standardisert, men dette påvirker ikke formen på mønsteret av prikker.

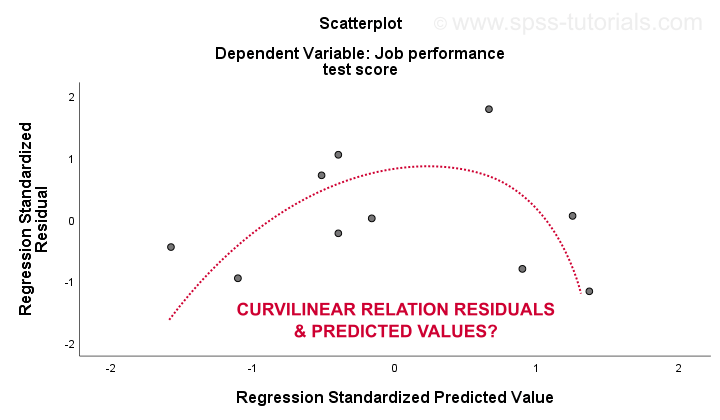
Ærlig, restplottet viser sterk krumlinearitet. Jeg trakk manuelt kurven som jeg tror passer best til det generelle mønsteret. Forutsatt at et krøllete forhold sannsynligvis løser heteroscedasticiteten også, men ting blir altfor teknisk nå.Det grunnleggende poenget er ganske enkelt at noen forutsetninger ikke holder.De vanligste løsningene for disse problemene – fra verste til beste-er

• ignorerer disse forutsetningene helt;
• lyver at regresjonsplottene ikke indikerer noen brudd på modellforutsetningene;
• en ikke-lineær transformasjon – som logaritmisk-til den avhengige variabelen;
• montering av en krøllete modell-som vi gir et skudd om et minutt.

TFO Retningslinjer For Rapportering Av Regresjon

figuren under er-bokstavelig talt – en lærebokillustrasjon for rapportering av regresjon I TFO-format.

Å Lage denne eksakte tabellen FRA SPSS-utgangen er en reell smerte i rumpa. Redigering det går lettere I Excel enn I WORD, slik at det kan spare deg for minst noen problemer.
Alternativt, prøv å komme unna med å kopiere lime inn (unedited) SPSS-utgangen og late som å være uvitende om det eksakte APA-formatet.

Non Linear Regression Experiment

vår utvalgsstørrelse er for liten til å passe noe utover en lineær modell. Men vi gjorde det likevel – bare nysgjerrighet. Det enkleste alternativet I SPSS er Under Analyser Regresjon Kurveestimering.Vi skal ikke diskutere dialogene, men vi limte inn syntaksen nedenfor.

SPSS Ikke-Lineær Regresjon Syntaks

Resultater

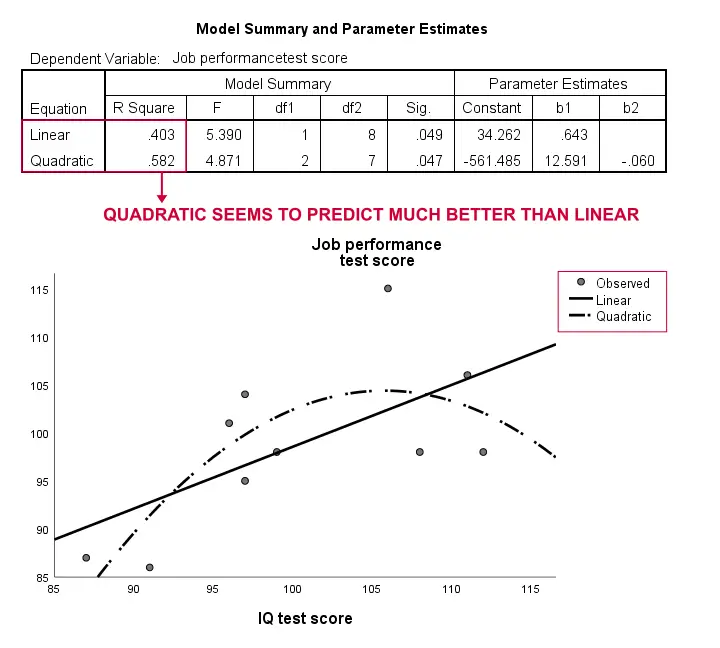
igjen er vårt utvalg altfor lite til å konkludere med noe seriøst. Resultatene tyder imidlertid på at en krøllete modell passer til dataene våre mye bedre enn den lineære. Vi vil ikke utforske dette lenger, men vi ville nevne det; vi føler at krøllete modeller rutinemessig overses av samfunnsvitere.

Takk for at du leste!