SPSS Simple Linear Regression Tutorial

SPSS Simple Linear Regression Tutorial

1. Fit Lineを使用した散布図の作成
2. SPSS線形回帰ダイアログ
3. SPSS回帰出力の解釈
4. 回帰仮定の評価
5. 回帰報告のためのAPAガイドライン

研究の質問とデータ

X社は10人の従業員にIqと仕事のパフォーマンステストを受けました。 結果のデータ（その一部を以下に示します）は、単純線形回帰です。サヴ

X社が把握したい主なものは、iqが仕事のパフォーマンスを予測することですか？ そして-もしそうなら-どのように？SPSSで簡単な線形回帰分析を実行することで、これらの質問に答えます。

近似線を使用した散布図の作成

分析の出発点は散布図です。 これは、IQとパフォーマンススコアとそれらの関係がある場合、最初は意味があるかどうかを教えてくれます。 グラフLegacy DialogsScatter/Dotからグラフを作成し、以下のスクリーンショットに従います。

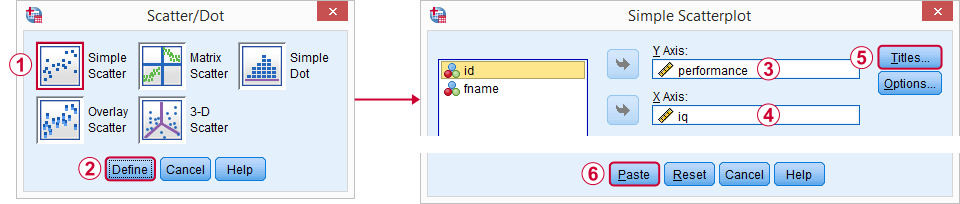
私は個人的に投げたいです

• 私の聴衆が基本的に何を見ているかを示すタイトルと、
• どの回答者や観察が表示され、どのように多くのことを示すサブタイトル。

ダイアログを歩くと、以下の構文が得られました。 それでは、それを実行してみましょう。

タイトル構文付きSPSS散布図

結果

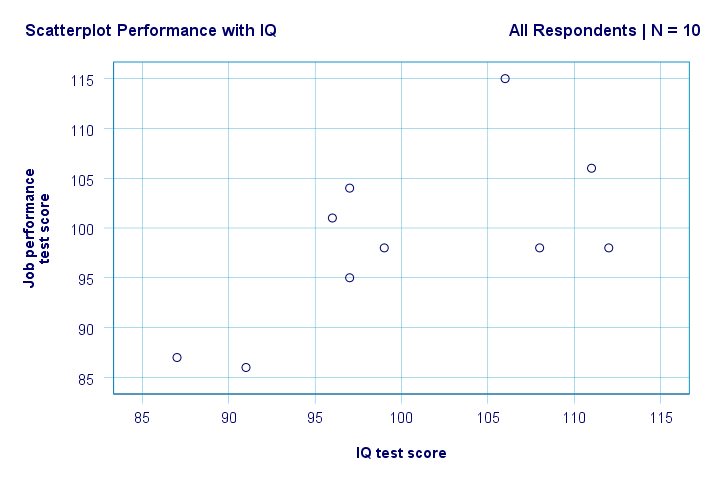
右。 最初に、散布図に奇妙なものは表示されません。 IQとパフォーマンスの間には中程度の相関関係があるようです: 平均して、より高いIQスコアを持つ回答者は、より良い実行されているように見えます。 この関係はほぼ線形に見えます。
散布図に回帰線を追加しましょう。 それを右クリックし、別のウィンドウでコンテンツの編集を選択すると、チャートエディタウィンドウが開きます。 ここでは、以下に示すように、単に”合計でフィットラインを追加”アイコンをクリックします。

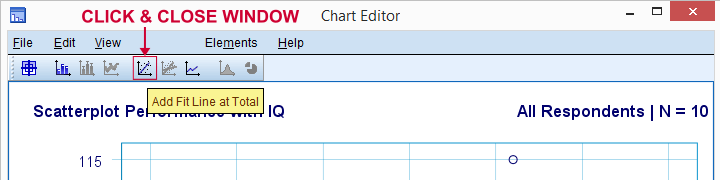
デフォルトでは、SPSSは散布図に線形回帰線を追加するようになりました。 その結果を以下に示します。

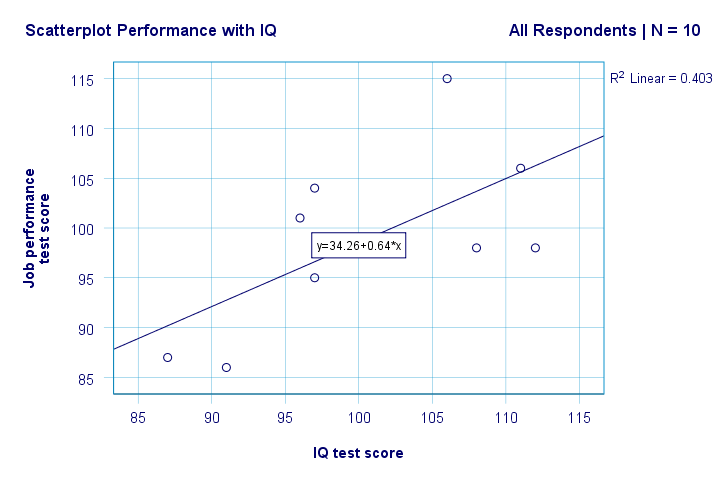
今、私たちの研究の質問に対する最初の基本的な答えがいくつかあります。 R2=0.403は、IQがパフォーマンススコアの分散の約40.3％を占めることを示します。 つまり、IQはこのサンプルでパフォーマンスをかなりよく予測します。
しかし、どのようにしてIQから仕事のパフォーマンスを最もよく予測できますか？ さて、散布図では、yはパフォーマンス（y軸に示されています）、xはIQ（x軸に示されています）です。 したがって、パフォーマンス=34.26+0.64*になりますIQ.So IQスコアが115の求職者の場合、私たちは次のように予測します34.26 + 0.64 * 115 =107彼/彼女の最も可能性の高い将来のパフォーマンススコアとして86。
そうなので、IQとパフォーマンスの関係についての基本的な考え方を与え、視覚的に提示します。 しかし、多くの情報-統計的有意性と信頼区間-はまだ欠けています。 だから行くとそれを取得してみましょう。

SPSS線形回帰ダイアログ

AnalyzeRegressionLinearから最小回帰分析を再実行すると、より詳細な出力が得られます。 以下のスクリーンショットは、私たちが続行する方法を示しています。

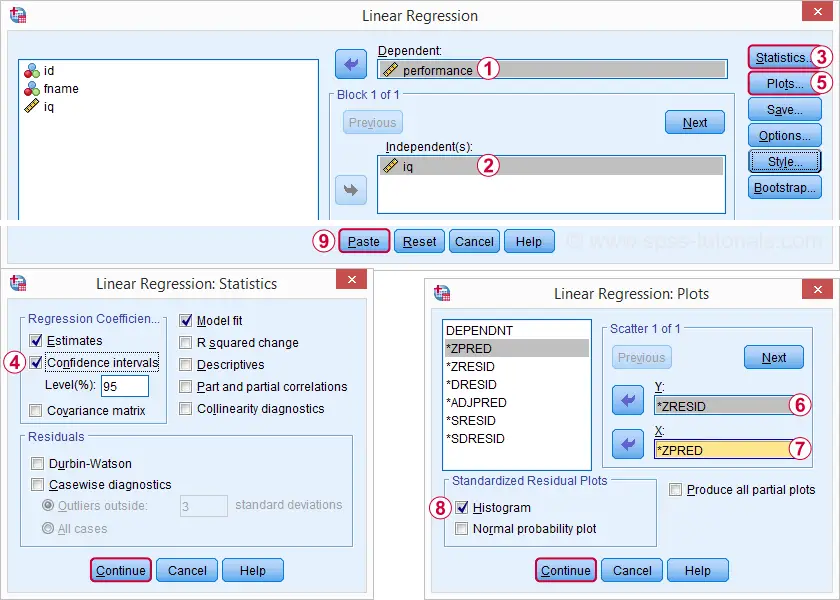
これらのオプションを選択すると、以下の構文になります。 それを実行してみましょう。

SPSS単純線形回帰構文

SPSS回帰出力I-Coefficients

残念ながら、SPSSは必要以上に多くの回帰出力を提供します。 私たちは安全にそれのほとんどを無視することができます。 しかし、主に重要な表は、以下に示す係数表である。

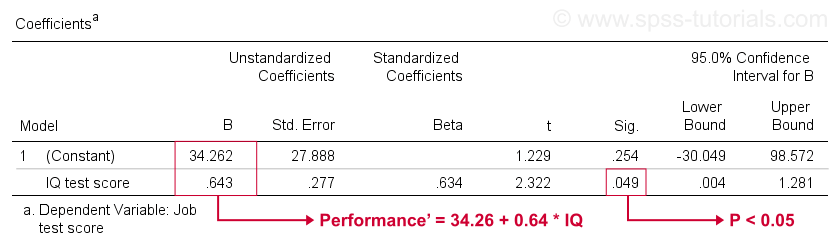
この表は、散布図で既に見たB係数を示しています。 示されているように、これらは、サンプルのIQからジョブのパフォーマンスを最もよく推定する線形回帰式を意味します。
第二に、p<0.05の場合、帰無仮説を棄却することを覚えておいてください。 IQのB係数は”Sig”またはp=0.049です。 ゼロとは統計的に有意に異なります。
しかし、その95％信頼区間-おおよそ、その母集団値の可能性の高い範囲-はである。 したがって、Bはおそらくゼロではありませんが、ゼロに非常に近いかもしれません。 信頼区間は巨大であり、Bの推定値はまったく正確ではなく、これは分析の基礎となる最小のサンプルサイズによるものです。

SPSS回帰出力II-モデルの要約

係数テーブルの他に、結果を報告するためのモデルの要約テーブルも必要です。

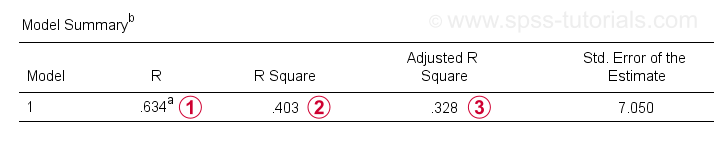
Rは回帰予測値と実際の値との相関です。 単純回帰の場合、Rは予測子と従属変数の間の相関に等しくなります。
R Square-二乗相関-は、サンプルデータの予測子によって説明される従属変数の分散の割合を示します。
調整されたR-squareは、（サンプルベースの）回帰式を母集団全体に適用するときにR-squareを推定します。
調整済みr平方は、単純なr平方よりも予測精度のより現実的な推定を提供します。 この例では、それらの間の大きな違い（一般的に収縮と呼ばれる）は、わずかN=10の非常に最小のサンプルサイズによるものです。
いずれにしても、これはX社にとって悪いニュースだ。IQは仕事のパフォーマンスを実際にはそれほどうまく予測していない。

回帰仮定の評価

回帰の主な仮定は

1. 独立観測値です。
2. 正規性：誤差は母集団の正規分布に従わなければなりません;
3. 線形性:各予測子と従属変数との関係は線形であり、
4. 等分散性:誤差は予測値のすべてのレベルにわたって一定の分散を持たなければなりません。

1. SPSSの各ケース（データビューのセルの行）が別々の人物を表す場合、通常、これらは「独立した観測」であると仮定します。 次に、仮定2-4は、出力の回帰プロットを調べることによって最もよく評価されます。

2. 正規性が保持されている場合、回帰残差は（おおよそ）正規分布する必要があります。 以下のヒストグラムは、正規性からの明確な逸脱を示していません。

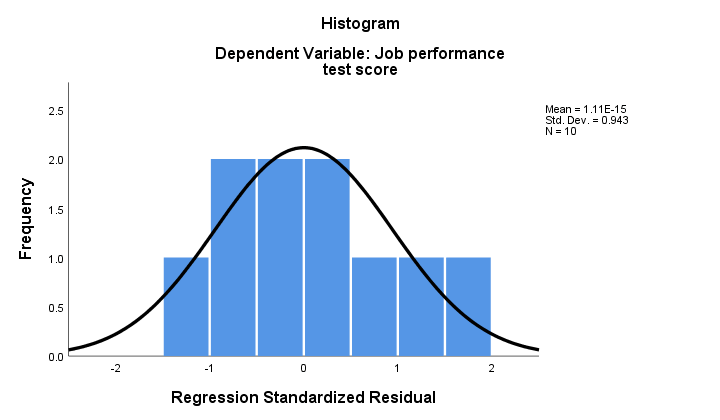
回帰手順では、これらの残差を新しい変数としてデータに追加できます。 そうすることで、Kolmogorov-Smirnovテストを実行して正規性を得ることができます。 しかし、手元にある小さなサンプルの場合、この検定は統計的検出力をほとんど持たないでしょう。 それでは、それをスキップしてみましょう。

の3 直線性および4. 相分散性の仮定は、残差プロットから最もよく評価されます。 これは、以下に示すように、x軸に予測値、y軸に残差を持つ散布図です。 両方の変数は標準化されていますが、これはドットのパターンの形状には影響しません。

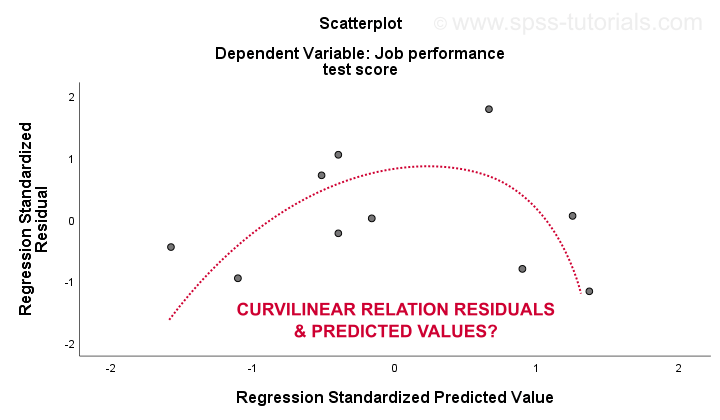
正直なところ、残差プロットは強い曲線性を示しています。 私は手動で私は最高の全体的なパターンに合うと思う曲線を描きました。 曲線関係を仮定すると、おそらく異方性も解決しますが、物事は今あまりにも技術的になっています。基本的なポイントは、単にいくつかの仮定が成立しないということです。これらの問題に対する最も一般的な解決策は、最悪から最高まで、これらの仮定を完全に無視する

• です。
• 回帰プロットはモデルの仮定の違反を示していないと嘘をついています。
• 従属変数への対数などの非線形変換。
• 曲線モデルをフィッティングします。これはすぐにショットを与えます。

回帰を報告するためのAPAガイドライン

下の図は、文字通り、APA形式の回帰を報告するための教科書の図です。

SPSS出力からこの正確なテーブルを作成することは、お尻の本当の痛みです。 WORDよりもExcelで編集する方が簡単になるため、少なくともいくつかの問題が解決する可能性があります。
あるいは、(編集されていない)SPSS出力をコピー-ペーストして、正確なAPA形式を知らないふりをしてみてください。

非線形回帰実験

サンプルサイズが小さすぎて、線形モデルを超えたものに実際に適合しません。 しかし、私たちはとにかくそうしました-ちょうど好奇心。 SPSSの最も簡単なオプションは、分析回帰曲線推定の下にあります。ダイアログについては説明しませんが、以下の構文を貼り付けました。

SPSS非線形回帰構文

結果

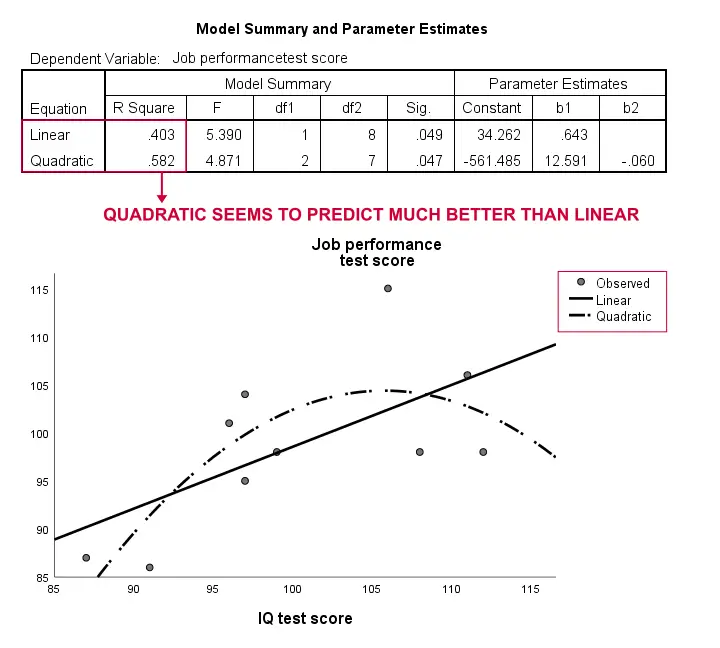
ここでも、サンプルは小さすぎて深刻なものを結論付けることはできません。 しかし、結果は、曲線モデルが線形モデルよりもはるかに優れたデータに適合することをちょっと示唆しています。 曲線モデルは社会科学者によって日常的に見落とされていると感じています。

読んでくれてありがとう！