高次の導関数を見つける方法
第二、第三、第四、またはより高い導関数を見つけることは非常に簡単です。 関数の二次導関数は、その一次導関数の導関数にすぎません。 第三の導関数は二次導関数の導関数であり、第四の導関数は第三の導関数であり、というようになります。
たとえば、ここでは関数とその第一、第二、第三、および後続の導関数です。 この例では、すべての導関数はべき乗則によって得られます:
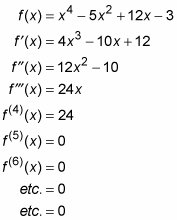
このようなすべての多項式関数は、繰り返し微分すると最終的にゼロになります。 一方、有理関数は次のようになります
あなたがより高く、より高い導関数を取るようにメシエとメシエを取得します。 そして、正弦と余弦の高次導関数は周期的です。 例えば,
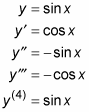
このサイクルは、四つの倍数ごとに無期限に繰り返されます。
一次導関数は、関数がどれくらい速く変化しているか、それがどれくらい速く上昇しているか、または下降しているかを示します。 二次導関数は、一次導関数がどのくらい速く変化しているか、つまり勾配がどのくらい速く変化しているかを示します。 三次導関数は、二次導関数がどのくらい速く変化しているかを示し、勾配の変化率がどのくらい速く変化しているかを示します。
ここで少し迷っているなら、心配しないでください。 あなたが二次導関数を過ぎて行くにつれて、より高い導関数があなたに伝えるものを扱うことはますます困難になります。




