SPSS egyszerű lineáris regresszió bemutató

SPSS egyszerű lineáris regresszió bemutató

1. Scatterplot létrehozása illeszkedő vonallal
2. SPSS lineáris regressziós párbeszédablakok
3. SPSS regressziós kimenet értelmezése
4. a regressziós feltételezések értékelése
5. APA iránymutatások a regresszió jelentéséhez

kutatási kérdés és adatok

X vállalat 10 alkalmazottal végzett IQ-és munkahelyi teljesítménytesztet. A kapott adatok – amelyek egy részét az alábbiakban mutatjuk be-egyszerű-lineáris-regresszióban vannak.sav.

a legfontosabb dolog, amit az X vállalat Ki akar találniaz IQ megjósolja a munka teljesítményét? És ha igen, hogyan?Ezekre a kérdésekre egy egyszerű lineáris regresszióanalízis futtatásával válaszolunk SPSS-ben.

Scatterplot létrehozása illesztési vonallal

elemzésünk nagyszerű kiindulópontja a scatterplot. Ez megmondja nekünk, hogy az IQ-nak és a teljesítmény pontszámoknak és azok viszonyának – ha van ilyen-van-e értelme. Diagramunkat grafikonokból készítjük Legacy Dialogs Scatter/Dot, majd követjük az alábbi képernyőképeket.

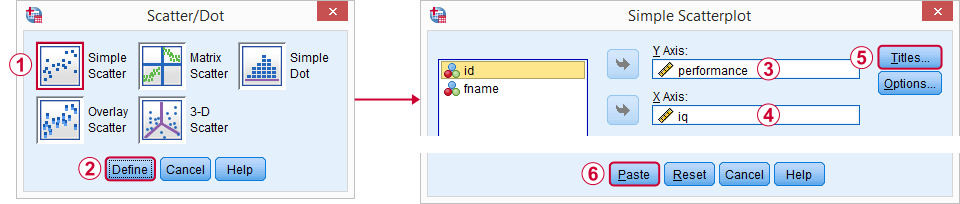
én személy szerint szeretem, hogy dobja be

• egy cím, amely azt mondja, amit a közönség alapvetően néz, és
• egy felirat, amely azt mondja, hogy mely válaszadók vagy megfigyelések jelennek meg, és hány.

a párbeszédablakok végigjárása az alábbi szintaxist eredményezte. Akkor futtassuk le.

SPSS Scatterplot címekkel szintaxis

eredmény

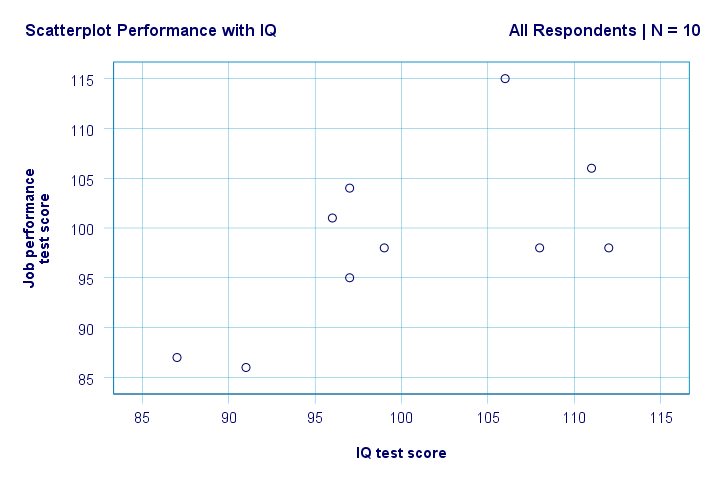
jobb. Tehát először, nem látunk semmi furcsát a szórásunkban. Úgy tűnik, hogy mérsékelt összefüggés van az IQ és a teljesítmény között: átlagban, a magasabb IQ-pontszámmal rendelkező válaszadók jobban teljesítenek. Ez a kapcsolat nagyjából lineárisnak tűnik.
most adjunk hozzá egy regressziós vonalat a szórásunkhoz. Kattintson rá a jobb gombbal, majd válassza a tartalom szerkesztése külön ablakban megnyílik egy Diagramszerkesztő ablak. Itt egyszerűen kattintson az” illeszkedési Vonal hozzáadása a teljes ” ikonra az alábbiak szerint.

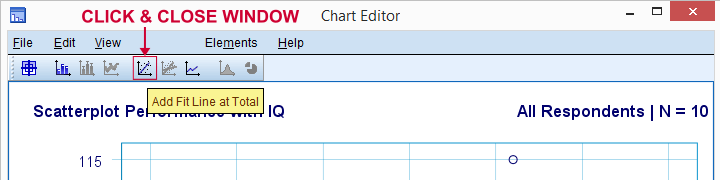
alapértelmezés szerint, SPSS most hozzáad egy lineáris regressziós egyenes a scatterplot. Az eredmény az alábbiakban látható.

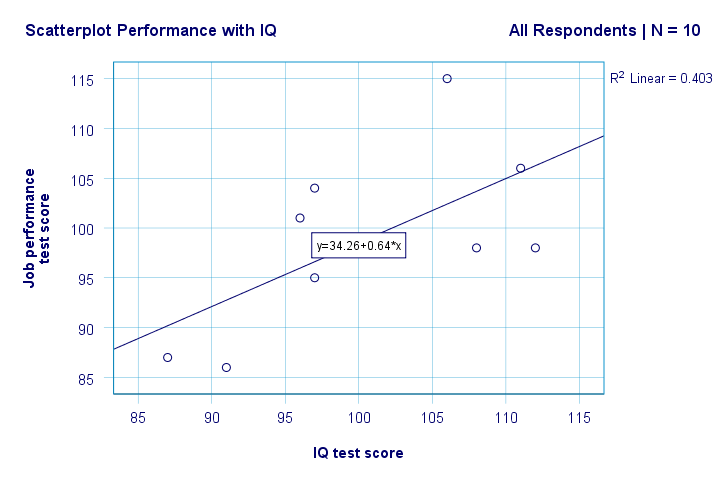
most már van néhány első alapvető válaszunk kutatási kérdéseinkre. R2 = 0,403 azt jelzi, hogy az IQ a teljesítmény pontszámok varianciájának mintegy 40,3% – át teszi ki. Vagyis az IQ meglehetősen jól megjósolja a teljesítményt ebben a mintában.
de hogyan lehet a legjobban megjósolni a munkahelyi teljesítményt az IQ-ból? Nos, a szórásunkban y a teljesítmény (az y tengelyen látható), x pedig IQ (az x tengelyen látható). Tehát ez leszteljesítmény = 34.26 + 0.64 * IQ.So egy 115-ös IQ-pontszámmal rendelkező pályázó számára megjósoljuk 34.26 + 0.64 * 115 = 107.86 mint a legvalószínűbb jövőbeli teljesítmény pontszáma.
rendben, tehát ez alapötletet ad nekünk az IQ és a teljesítmény közötti kapcsolatról, és vizuálisan mutatja be. Azonban sok információ-statisztikai szignifikancia és konfidencia intervallumok-még mindig hiányzik. Akkor menjünk és szerezzük meg.

SPSS lineáris regressziós párbeszédablakok

a minimális regresszióanalízisünk újrafuttatása az analize regresszió lineáris sokkal részletesebb kimenetet ad nekünk. Az alábbi képernyőképek megmutatják, hogyan folytatjuk.

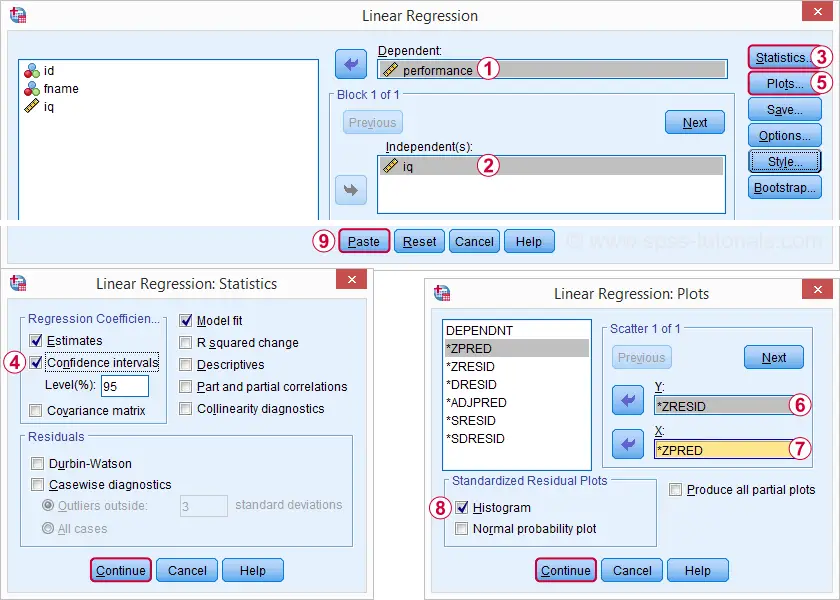
ezen opciók kiválasztása az alábbi szintaxist eredményezi. Futtassuk le.

SPSS egyszerű lineáris regressziós szintaxis

SPSS regressziós kimenet I-együtthatók

sajnos az SPSS sokkal több regressziós kimenetet ad nekünk, mint amennyire szükségünk van. A legtöbbet nyugodtan figyelmen kívül hagyhatjuk. A nagy jelentőségű táblázat azonban az alábbi együtthatók táblázata.

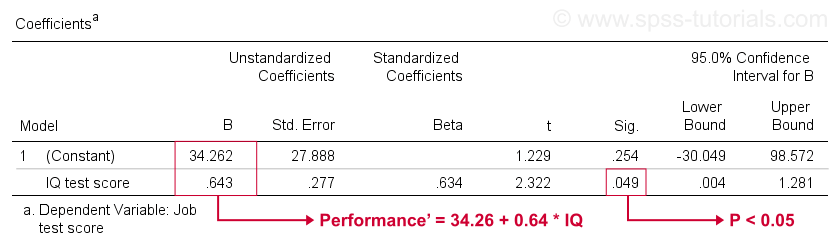
ez a táblázat azokat a B-együtthatókat mutatja, amelyeket már láttunk a szórásunkban. Mint jeleztük, ezek azt a lineáris regressziós egyenletet jelentik, amely a mintánkban az IQ alapján a legjobban becsüli a munkateljesítményt.
másodszor, ne feledje, hogy általában elutasítjuk a nullhipotézist, ha p < 0,05. Az IQ B együtthatója ” Sig ” vagy p = 0,049. Statisztikailag szignifikánsan különbözik a nullától.
azonban a 95% – os konfidencia-intervallum-nagyjából a populáció értékének valószínű tartománya-az . Tehát B valószínűleg nem nulla, de nagyon közel lehet a nullához. A konfidencia intervallum hatalmas -becslésünk B – re egyáltalán nem pontos -, és ez annak a minimális mintaméretnek köszönhető, amelyen az elemzés alapul.

SPSS regressziós kimenet II – modell összefoglaló

az együtthatók táblázatán kívül szükségünk van a modell összefoglaló táblázatra is eredményeink jelentéséhez.

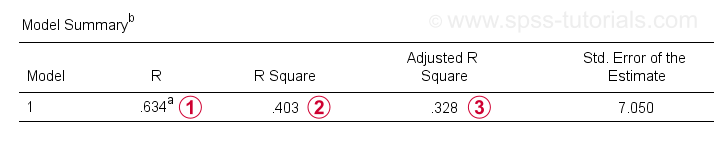
R a regresszió által előre jelzett értékek és a tényleges értékek közötti korreláció. Egyszerű regresszió esetén R egyenlő a prediktor és a függő változó közötti korrelációval.
R négyzet -a négyzetes korreláció-jelzi a variancia arányát a függő változóban, amelyet a prediktor(ok) számolnak el a mintaadatainkban.
Korrigált R-négyzet becslések R-négyzet, amikor a (minta alapú) regressziós egyenletünket alkalmazzuk a teljes populációra.
a korrigált r-négyzet reálisabb becslést ad a prediktív pontosságról, mint egyszerűen az r-négyzet. Példánkban a köztük lévő nagy különbség-általában zsugorodásnak nevezik-annak köszönhető, hogy nagyon minimális mintanagyságunk csak N = 10.
mindenesetre ez rossz hír az X vállalat számára: az IQ végül is nem igazán jósolja meg olyan szépen a munkateljesítményt.

a regressziós feltételezések értékelése

a regresszió fő feltételezései

1. független megfigyelések;
2. normalitás: a hibáknak normális eloszlást kell követniük a populációban;
3. linearitás: az egyes prediktorok és a függő változó közötti kapcsolat lineáris;
4. Homoszkedaszticitás: a hibáknak állandó varianciával kell rendelkezniük a megjósolt érték minden szintjén.

1. Ha az SPSS-ben minden egyes eset (cellasor adatnézetben) külön személyt képvisel, akkor általában feltételezzük, hogy ezek “független megfigyelések”. Ezután a 2-4 feltételezéseket a kimenetünk regressziós diagramjainak ellenőrzésével lehet a legjobban értékelni.

2. Ha a normalitás fennáll, akkor a regressziós maradványainknak (nagyjából) normálisan kell eloszlaniuk. Az alábbi hisztogram nem mutat egyértelmű eltérést a normalitástól.

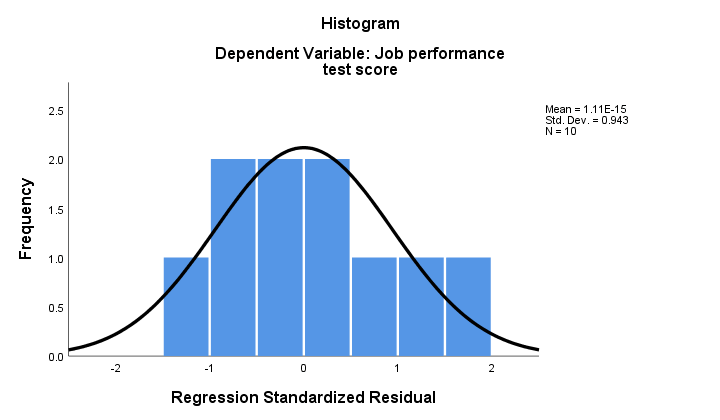
a regressziós eljárás ezeket a maradványokat új változóként adhatja hozzá az adatokhoz. Ezzel lefuttathat egy Kolmogorov-Szmirnov tesztet a normalitásra. A kéznél lévő apró minta esetében azonban ennek a tesztnek alig lesz statisztikai ereje. Szóval hagyjuk ki.

az 3. linearitás és 4. a homoszkedaszticitási feltételezéseket legjobban egy maradék parcellából lehet értékelni. Ez egy szórás, amelynek előre jelzett értékei vannak az x tengelyen,a maradványok pedig az y tengelyen, az alábbiak szerint. Mindkét változót szabványosították, de ez nem befolyásolja a pontok mintázatának alakját.

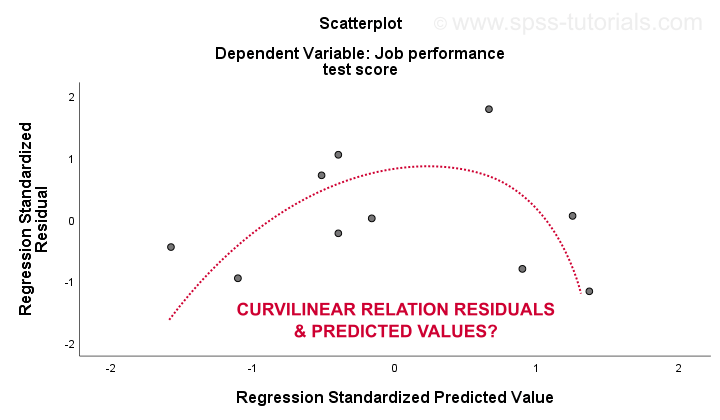
őszintén szólva, a maradék telek erős görbületességet mutat. Kézzel rajzoltam azt a görbét, amely szerintem a legjobban illeszkedik az Általános mintához. Feltételezve, hogy egy görbe vonalú kapcsolat valószínűleg megoldja a heteroszkedaszticitást is, de a dolgok most már túl technikai jellegűek.Az alapvető pont egyszerűen az, hogy egyes feltételezések nem állnak fenn.A leggyakoribb megoldás ezekre a problémákra – a legrosszabbtól a legjobbig-a

• figyelmen kívül hagyva ezeket a feltételezéseket;
• hazudva, hogy a regressziós diagramok nem jelzik a modellfeltevések megsértését;
• nem lineáris transzformáció-például logaritmikus – a függő változóra;
• görbe vonalú modell illesztése-amelyet egy perc alatt adunk.

APA iránymutatások a regresszió jelentéséhez

az alábbi ábra-szó szerint – tankönyvi illusztráció a regresszió APA formátumban történő jelentéséhez.

ennek a pontos táblázatnak az SPSS kimenetből történő létrehozása valódi fájdalom a szamárban. Szerkesztése megy könnyebb Excel, mint a WORD, így lehet menteni egy legalább néhány baj.
Alternatív megoldásként próbálja meg megúszni a (szerkesztetlen) SPSS kimenet másolását, és tegyen úgy, mintha nem lenne tisztában a pontos APA formátummal.

nem lineáris regressziós kísérlet

a minta mérete túl kicsi ahhoz, hogy valóban illeszkedjen semmit túl lineáris modell. De így is tettük-csak kíváncsiság. A legegyszerűbb lehetőség az SPSS-ben az Analyze regresszió görbe becslés alatt található.Nem fogjuk megvitatni a párbeszédablakokat, de beillesztettük az alábbi szintaxist.

SPSS nemlineáris regressziós szintaxis

eredmények

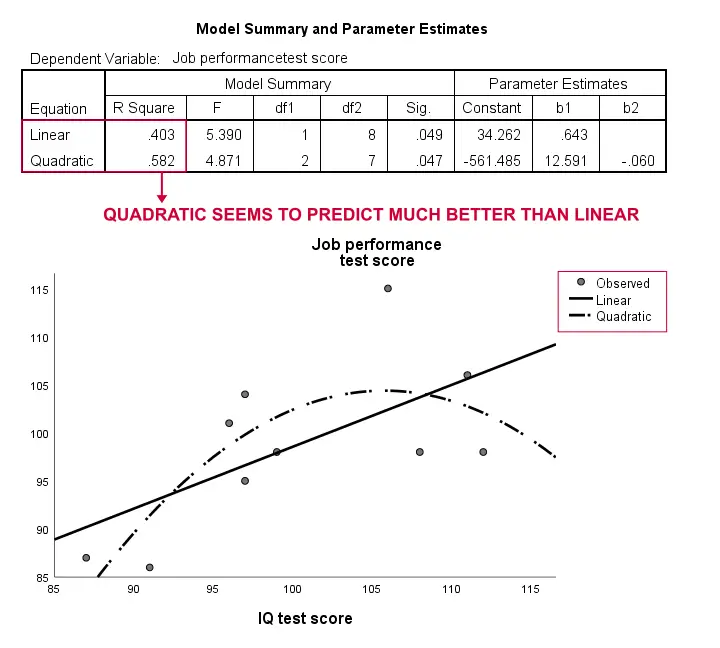
ismét a mintánk túl kicsi ahhoz, hogy bármi komoly következtetést vonjunk le. Az eredmények azonban azt sugallják, hogy egy görbe vonalú modell sokkal jobban illeszkedik az adatainkhoz, mint a lineáris. Ezt nem fogjuk tovább vizsgálni, de meg akartuk említeni; úgy érezzük, hogy a görbületi modelleket a társadalomtudósok rutinszerűen figyelmen kívül hagyják.

köszönöm az olvasást!