Tutoriel de Régression Linéaire Simple SPSS

Tutoriel de Régression Linéaire Simple SPSS

1. Créer un Nuage de points avec une Ligne d’ajustement
2. Boîtes de Dialogue de Régression Linéaire SPSS
3. Interprétation de la Sortie de Régression SPSS
4. Évaluation des hypothèses de régression
5. Lignes directrices de l’APA pour Signaler la régression

Question de recherche et données

L’entreprise X a demandé à 10 employés de passer un test de QI et de performance au travail. Les données résultantes – dont une partie est illustrée ci-dessous – sont en régression linéaire simple.sav.

La principale chose que la société X veut comprendre est-ce que IQ prédit la performance au travail? Et – si oui – comment?Nous répondrons à ces questions en exécutant une analyse de régression linéaire simple dans SPSS.

Créer un nuage de points avec la ligne d’ajustement

Un excellent point de départ pour notre analyse est un nuage de points. Cela nous dira si les scores de QI et de performance et leur relation – le cas échéant – ont un sens en premier lieu. Nous allons créer notre tableau à partir de Graphiques Boîtes de dialogue héritées Scatter / Dot et nous suivrons ensuite les captures d’écran ci-dessous.

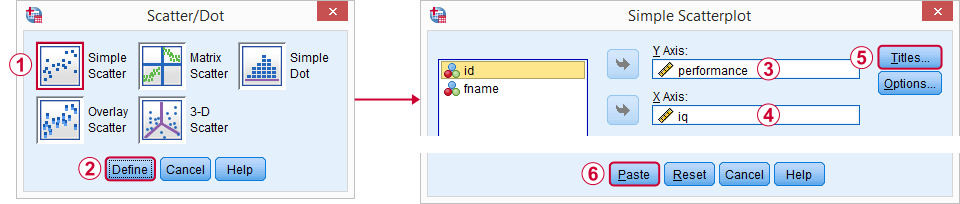
J’aime personnellement lancer

• un titre qui dit ce que mon public regarde fondamentalement et
• un sous-titre qui dit quels répondants ou observations sont montrés et combien.

Parcourir les boîtes de dialogue a abouti à la syntaxe ci-dessous. Alors allons-y.

Nuage de points SPSS avec Syntaxe des titres

Résultat

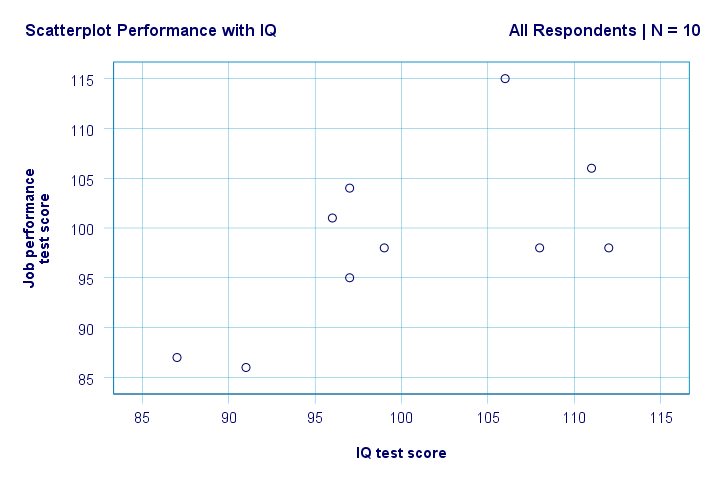
Droite. Donc tout d’abord, nous ne voyons rien de bizarre dans notre nuage de points. Il semble y avoir une corrélation modérée entre le QI et les performances: en moyenne, les répondants ayant des scores de QI plus élevés semblent avoir de meilleurs résultats. Cette relation semble à peu près linéaire.
Ajoutons maintenant une ligne de régression à notre nuage de points. En cliquant dessus avec le bouton droit de la souris et en sélectionnant Modifier le contenu Dans une fenêtre séparée, une fenêtre d’éditeur de graphiques s’ouvre. Ici, nous cliquons simplement sur l’icône « Ajouter une ligne d’ajustement au total » comme indiqué ci-dessous.

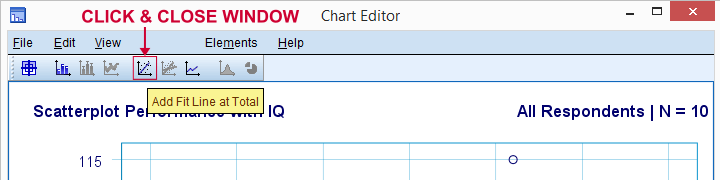
Par défaut, SPSS ajoute maintenant une ligne de régression linéaire à notre nuage de points. Le résultat est montré ci-dessous.

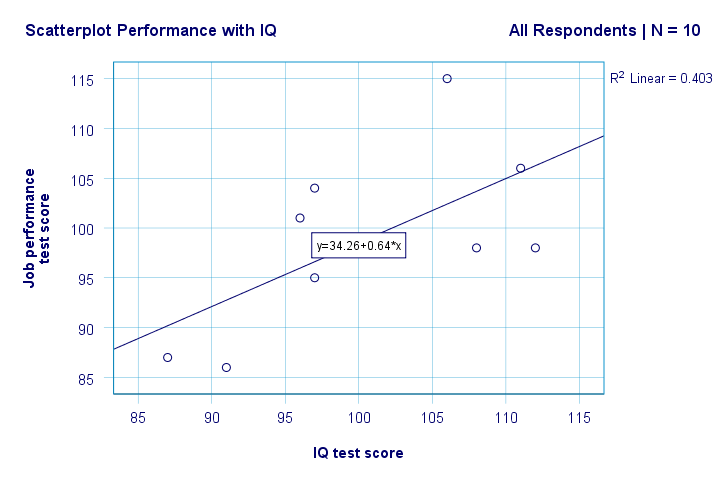
Nous avons maintenant quelques premières réponses de base à nos questions de recherche. R2 = 0,403 indique que le QI représente environ 40,3% de la variance des scores de performance. Autrement dit, IQ prédit assez bien les performances dans cet échantillon.
Mais comment pouvons-nous prédire au mieux les performances au travail à partir du QI? Eh bien, dans notre nuage de points, y est la performance (indiquée sur l’axe des ordonnées) et x est IQ (indiquée sur l’axe des abscisses). Donc ce seraperformance = 34,26 + 0,64 * IQ.So pour un candidat avec un score de QI de 115, nous allons prédire 34.26 + 0.64 * 115 = 107.86 comme son score de performance future le plus probable.
C’est vrai, cela nous donne une idée de base sur la relation entre le QI et la performance et la présente visuellement. Cependant, beaucoup d’informations – signification statistique et intervalles de confiance – manquent encore. Alors allons le chercher.

Boîtes de dialogue de régression linéaire SPSS

Réexécuter notre analyse de régression minimale à partir d’Analyser Régression Linéaire nous donne une sortie beaucoup plus détaillée. Les captures d’écran ci-dessous montrent comment nous allons procéder.

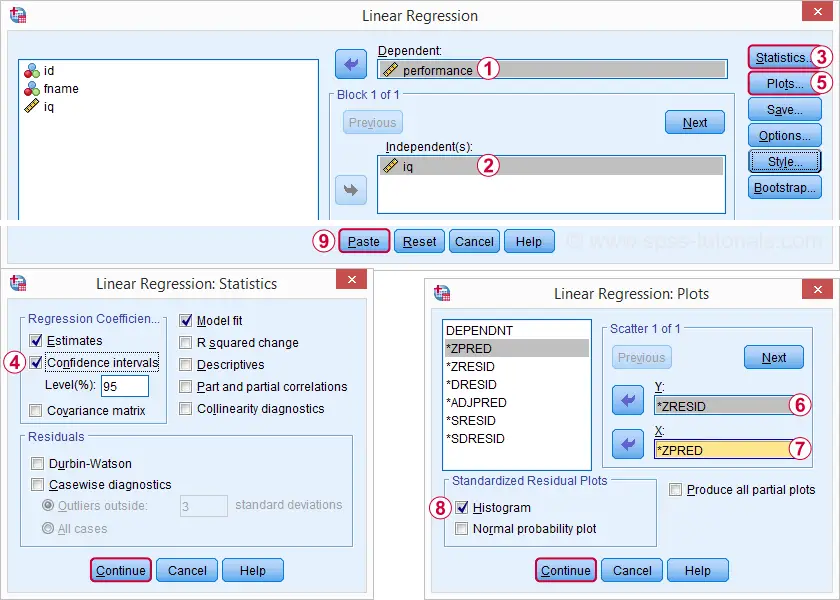
La sélection de ces options donne la syntaxe ci-dessous. Allons-y.

Syntaxe de régression linéaire simple SPSS

Sortie de régression SPSS I-Coefficients

Malheureusement, SPSS nous donne beaucoup plus de sortie de régression que nous n’en avons besoin. Nous pouvons en ignorer la plupart en toute sécurité. Cependant, un tableau d’importance majeure est le tableau des coefficients ci-dessous.

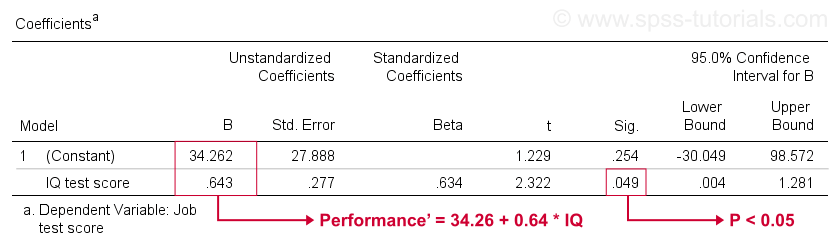
Ce tableau montre les coefficients B que nous avons déjà vus dans notre nuage de points. Comme indiqué, ceux-ci impliquent l’équation de régression linéaire qui estime le mieux le rendement au travail à partir du QI dans notre échantillon.
Deuxièmement, rappelez-vous que nous rejetons généralement l’hypothèse nulle si p < 0,05. Le coefficient B pour le QI a « Sig » ou p = 0,049. C’est statistiquement significativement différent de zéro.
Cependant, son intervalle de confiance à 95% – à peu près, une fourchette probable pour sa valeur de population – est. Donc B n’est probablement pas zéro mais il pourrait bien être très proche de zéro. L’intervalle de confiance est énorme – notre estimation pour B n’est pas précise du tout – et cela est dû à la taille minimale de l’échantillon sur lequel l’analyse est basée.

Sortie de régression SPSS II – Résumé du modèle

Outre le tableau des coefficients, nous avons également besoin du tableau récapitulatif du modèle pour rendre compte de nos résultats.

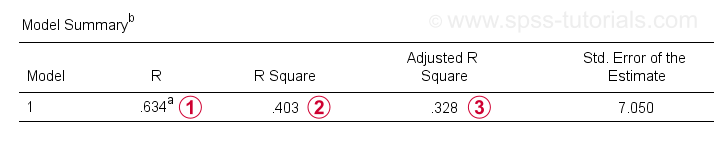
R est la corrélation entre les valeurs prédites de régression et les valeurs réelles. Pour une régression simple, R est égal à la corrélation entre le prédicteur et la variable dépendante.
Le carré R – la corrélation au carré – indique la proportion de variance dans la variable dépendante qui est prise en compte par le ou les prédicteurs dans nos données d’échantillon.
Estimations R-carré ajustées R-carré lors de l’application de notre équation de régression (basée sur l’échantillon) à l’ensemble de la population.
Le carré r ajusté donne une estimation plus réaliste de la précision prédictive qu’un simple carré r. Dans notre exemple, la grande différence entre eux – généralement appelée rétrécissement – est due à notre taille d’échantillon très minimale de seulement N = 10.
En tout cas, c’est une mauvaise nouvelle pour l’entreprise X: IQ ne prédit pas vraiment les performances au travail après tout.

Évaluation des hypothèses de régression

Les principales hypothèses de régression sont

1. Observations indépendantes;
2. Normalité : les erreurs doivent suivre une distribution normale dans la population;
3. Linéarité: la relation entre chaque prédicteur et la variable dépendante est linéaire;
4. Homoscédasticité: les erreurs doivent avoir une variance constante sur tous les niveaux de valeur prédite.

1. Si chaque cas (ligne de cellules dans la vue des données) dans SPSS représente une personne distincte, nous supposons généralement qu’il s’agit d' »observations indépendantes ». Ensuite, les hypothèses 2 à 4 sont mieux évaluées en inspectant les graphiques de régression dans notre production.

2. Si la normalité se maintient, alors nos résidus de régression devraient être (à peu près) normalement distribués. L’histogramme ci-dessous ne montre pas un écart clair par rapport à la normalité.

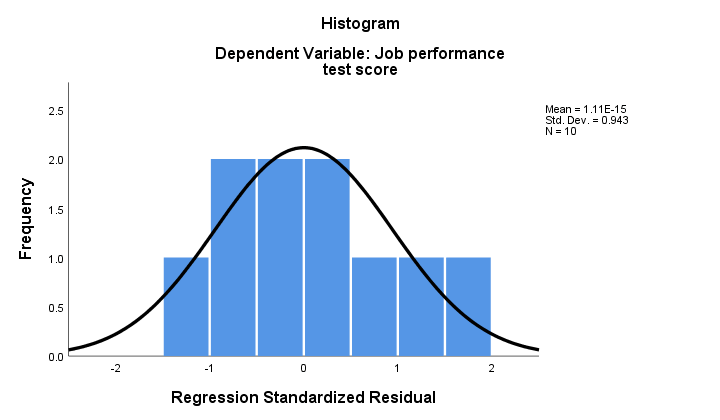
La procédure de régression peut ajouter ces résidus en tant que nouvelle variable à vos données. Ce faisant, vous pourriez exécuter un test de Kolmogorov-Smirnov pour la normalité sur eux. Pour le petit échantillon à portée de main, cependant, ce test n’aura guère de puissance statistique. Alors sautons-le.

La 3. linéarité et 4. les hypothèses d’homoscédasticité sont mieux évaluées à partir d’un graphique résiduel. Il s’agit d’un nuage de points avec des valeurs prédites sur l’axe des abscisses et des résidus sur l’axe des ordonnées, comme indiqué ci-dessous. Les deux variables ont été normalisées, mais cela n’affecte pas la forme du motif des points.

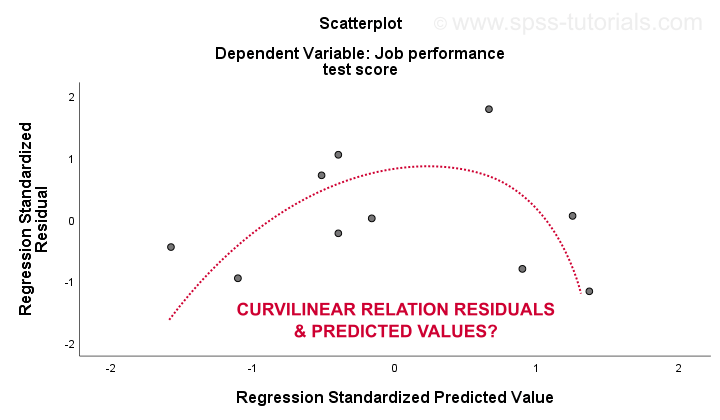
Honnêtement, la courbe résiduelle montre une forte curvilinéarité. J’ai dessiné manuellement la courbe qui, je pense, correspond le mieux au motif général. En supposant qu’une relation curviligne résout probablement aussi l’hétéroscédasticité, mais les choses deviennent beaucoup trop techniques maintenant.Le point de base est simplement que certaines hypothèses ne tiennent pas.Les solutions les plus courantes pour ces problèmes – du pire au meilleur – sont

• en ignorant complètement ces hypothèses;
• en mentionnant que les graphiques de régression n’indiquent aucune violation des hypothèses du modèle;
• une transformation non linéaire – telle que logarithmique – en variable dépendante;
• en ajustant un modèle curviligne – que nous allons essayer dans une minute.

Lignes directrices de l’APA pour la déclaration de régression

La figure ci-dessous est – littéralement – une illustration de manuel pour la déclaration de régression au format APA.

Créer cette table exacte à partir de la sortie SPSS est une vraie douleur dans le cul. L’édition est plus facile dans Excel que dans WORD, ce qui peut vous éviter au moins quelques problèmes.
Sinon, essayez de copier-coller la sortie SPSS (non éditée) et faites semblant d’ignorer le format APA exact.

Expérience de régression non linéaire

La taille de notre échantillon est trop petite pour s’adapter réellement à quelque chose au-delà d’un modèle linéaire. Mais nous l’avons fait de toute façon – juste de la curiosité. L’option la plus simple dans SPSS est sous Analyser Régression Estimation de la courbe.Nous n’allons pas discuter des boîtes de dialogue mais nous avons collé la syntaxe ci-dessous.

Syntaxe de Régression Non linéaire SPSS

Résultats

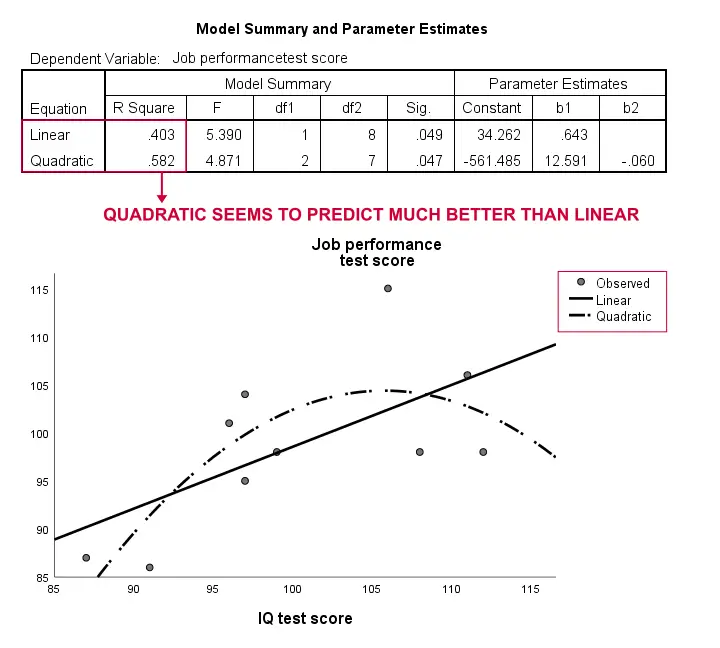
Encore une fois, notre échantillon est bien trop petit pour conclure à quelque chose de sérieux. Cependant, les résultats suggèrent un peu qu’un modèle curviligne correspond beaucoup mieux à nos données que le modèle linéaire. Nous n’explorerons pas cela plus loin, mais nous voulions le mentionner; nous pensons que les modèles curvilignes sont régulièrement négligés par les spécialistes des sciences sociales.

Merci d’avoir lu!