Comment trouver des Dérivés d’Ordre Élevé
Trouver un dérivé de deuxième, troisième, quatrième ou supérieur est incroyablement simple. La dérivée seconde d’une fonction n’est que la dérivée de sa dérivée première. La troisième dérivée est la dérivée de la dérivée seconde, la quatrième dérivée est la dérivée de la troisième, et ainsi de suite.
Par exemple, voici une fonction et ses première, deuxième, troisième et dérivées suivantes. Dans cet exemple, toutes les dérivées sont obtenues par la règle de puissance:
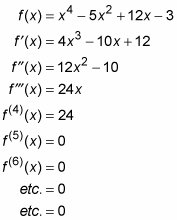
Toutes les fonctions polynomiales comme celle-ci finissent par passer à zéro lorsque vous vous différenciez à plusieurs reprises. D’autre part, les fonctions rationnelles comme
obtenez messier et messier lorsque vous prenez des dérivés de plus en plus élevés. Et les dérivés supérieurs du sinus et du cosinus sont cycliques. Par exemple,
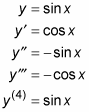
Le cycle se répète indéfiniment avec tous les multiples de quatre.
Une dérivée première vous indique à quelle vitesse une fonction change — à quelle vitesse elle monte ou descend — c’est sa pente. Une dérivée seconde vous indique à quelle vitesse la dérivée première change — ou, en d’autres termes, à quelle vitesse la pente change. Une dérivée troisième vous indique à quelle vitesse la dérivée seconde change, ce qui vous indique à quelle vitesse le taux de changement de la pente change.
Si vous vous perdez un peu ici, ne vous inquiétez pas. Il devient de plus en plus difficile de comprendre ce que les dérivés plus élevés vous disent au fur et à mesure que vous dépassez la dérivée seconde, parce que vous commencez à entrer dans un taux de changement d’un taux de changement d’un taux de changement, et ainsi de suite.




