SPSS Simple Linear Regression Tutorial

SPSS Simple Linear Regression Tutorial

1. Create Scatterplot with Fit Line
2. SPSS Linear Regression dialogit
3. Interpreting SPSS Regression Output
4. Evaluating the Regression oletukset
5. apa Guidelines for Reporting Regression

tutkimuskysymys ja tiedot

yritys X teetti 10 työntekijälle älykkyysosamäärä-ja Työsuoritustestin. Tuloksena olevat tiedot – joista osa on esitetty alla-ovat yksinkertaisessa lineaarisessa regressiossa.sav.

the main thing Company X wants to figure out isdoes IQ predict job performance? Ja-jos on-miten?Vastaamme näihin kysymyksiin suorittamalla yksinkertaisen lineaarisen regressioanalyysin SPSS: ssä.

Create Scatterplot with Fit Line

a great startup for our analysis is a scatterplot. Tämä kertoo, onko ÄLYKKYYSOSAMÄÄRISSÄ ja suoritustasoissa ja niiden suhteessa – jos ollenkaan-ylipäätään mitään järkeä. Luomme kaavion graafeista Legacy-dialogit Scatter/Dot ja seuraamme sitten alla olevia kuvakaappauksia.

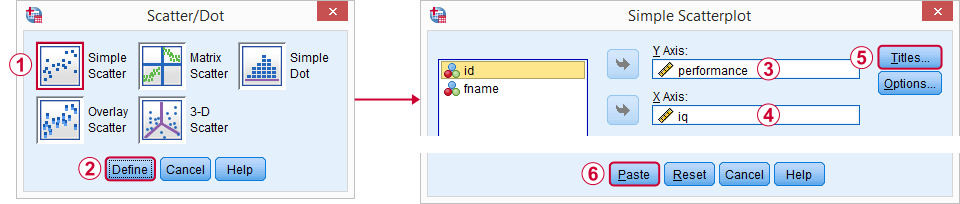
itse tykkään heittää

• otsikko, joka kertoo, mitä yleisöni periaatteessa katsoo, ja
• alaotsikko, joka kertoo, ketkä vastaajat tai havainnot näytetään ja kuinka monta.

dialogien läpi Käveleminen johti alla olevaan syntaksiin. Kokeillaan sitä.

SPSS-Scatterplot otsikoiden syntaksilla

tulos

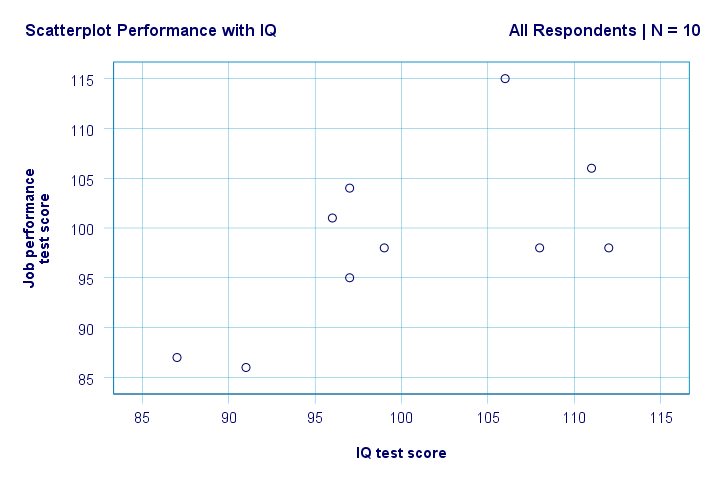
Right. Ensinnäkin, emme näe mitään outoa scatterplotissamme. Älykkyysosamäärän ja suorituskyvyn välillä näyttää olevan kohtalainen korrelaatio: keskimäärin vastaajat, joilla on korkeampi älykkyysosamäärä, näyttävät suoriutuvan paremmin. Suhde näyttää suunnilleen lineaariselta.
lisätään nyt regressiorivi scatterplotiin. Napsauttamalla sitä hiiren kakkospainikkeella ja valitsemalla Edit content erillisessä ikkunassa avautuu karttaeditori-ikkuna. Täällä me yksinkertaisesti klikkaa ”Lisää sovitus rivi yhteensä”kuvake kuten alla.

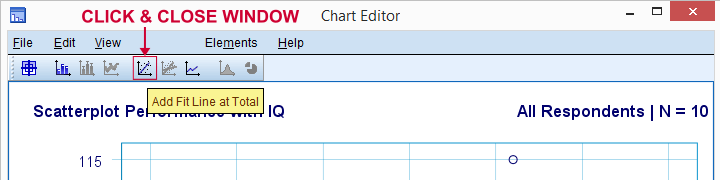
by default, SPSS now adds a linear regression line to our scatterplot. Tulos on esitetty alla.

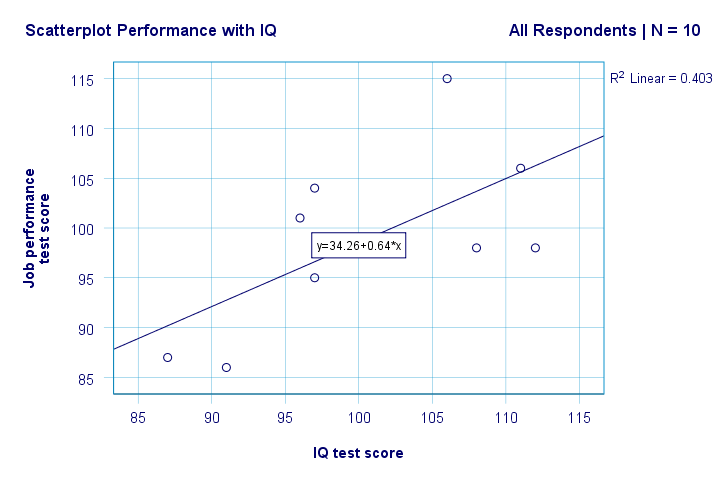
meillä on nyt joitakin ensimmäisiä perusvastauksia tutkimuskysymyksiimme. R2 = 0,403 osoittaa, että älykkyysosamäärä muodostaa noin 40,3% suorituspisteiden varianssista. Eli älykkyysosamäärä ennustaa suoritusta melko hyvin tässä otoksessa.
mutta miten voimme parhaiten ennustaa työsuorituksen ÄLYKKYYSOSAMÄÄRÄSTÄ? No, meidän scatterplot y on suorituskyky (näkyy y-akselilla) ja x on IQ (näkyy x-akselilla). Eli se on suoritus = 34,26 + 0,64 * IQ.So työnhakijalle, jonka älykkyysosamäärä on 115, ennustamme 34.26 + 0.64 * 115 = 107.86 hänen todennäköisimpänä tulevana suoritusarvosananaan.
oikein, joten se antaa meille perusidean älykkyysosamäärän ja suorituskyvyn suhteesta ja esittää sen visuaalisesti. Paljon tietoa-tilastollista merkitsevyyttä ja luottamusvälejä – kuitenkin vielä puuttuu. Mennään hakemaan se.

SPSS Linear Regression dialogit

minimaalisen regressioanalyysin uusiminen Analyzistä regressio Linear antaa meille paljon yksityiskohtaisemman tuotoksen. Alla olevat kuvakaappaukset näyttävät, miten edetään.

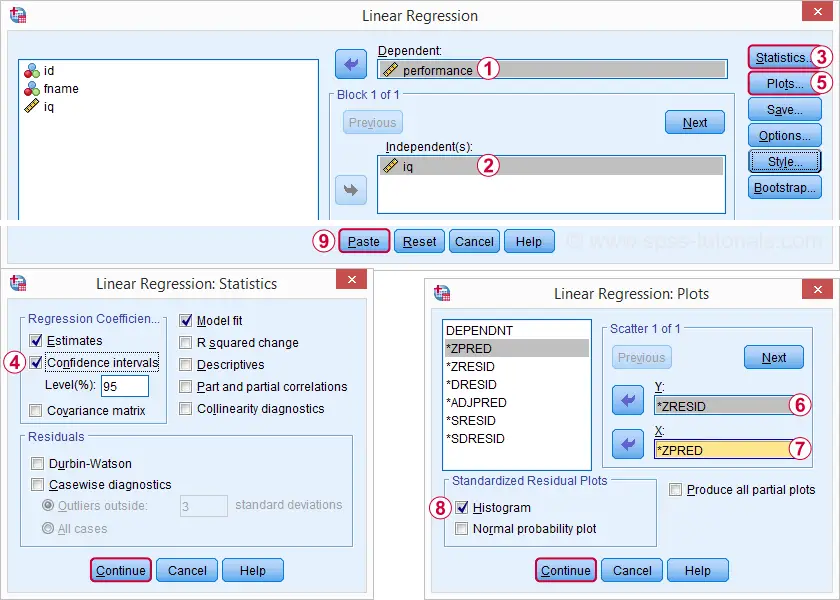
näiden vaihtoehtojen valitseminen johtaa alla olevaan syntaksiin. Tehdään se.

SPSS yksinkertainen lineaarinen regressio syntaksi

SPSS Regressiotuotos I – kertoimet

valitettavasti SPSS antaa meille paljon enemmän regressiotuotosta kuin tarvitsemme. Voimme huoletta jättää suurimman osan huomiotta. Kuitenkin taulukko on erittäin tärkeä On kertoimet taulukossa alla.

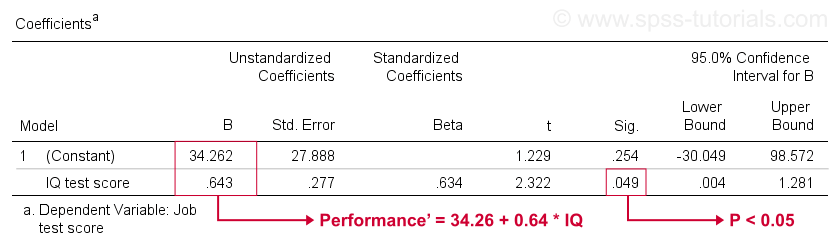
tämä taulukko esittää ne b-kertoimet, jotka näimme jo scatterplotissamme. Kuten edellä, nämä merkitsevät lineaarinen regressioyhtälö, joka parhaiten arvioi työn suorituskykyä älykkyysosamäärä meidän näyte.
toiseksi, muista, että yleensä hylkäämme nollahypoteesin, jos p < 0,05. Älykkyysosamäärän B-kerroin on ” Sig ” eli p = 0,049. Se eroaa tilastollisesti merkittävästi nollasta.
sen 95 prosentin luottamusväli on kuitenkin suurin piirtein populaatioarvon todennäköinen vaihteluväli . B ei siis todennäköisesti ole nolla, mutta se voi hyvinkin olla hyvin lähellä nollaa. Luottamusväli on valtava-arviomme B: lle ei ole lainkaan tarkka – ja tämä johtuu minimaalisesta otoskoosta, johon analyysi perustuu.

SPSS Regressiolähtö II-mallin Yhteenveto

kerrointaulukon lisäksi tarvitsemme myös mallin yhteenvetotaulukon tulosten raportointia varten.

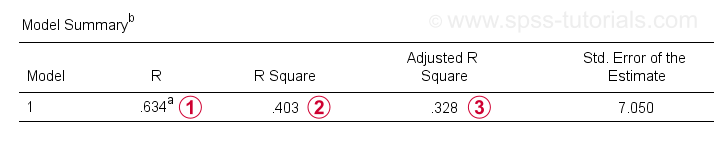
R on ennustettujen regressioarvojen ja todellisten arvojen välinen korrelaatio. Yksinkertaisessa regressiossa R on yhtä suuri kuin predikaattorin ja riippuvan muuttujan välinen korrelaatio.
R neliö-neliökorrelaatio-ilmaisee riippuvan muuttujan varianssin osuuden, jonka predikaattori(t) selittää otosaineistossamme.
oikaistu R-neliön estimaatti R-neliö, kun sovelletaan (otokseen perustuvaa) regressioyhtälöämme koko populaatioon.
mukautettu r-neliö antaa realistisemman arvion ennustavasta tarkkuudesta kuin pelkkä R-neliö. Esimerkissämme suuri ero niiden välillä-jota yleensä kutsutaan kutistumiseksi-johtuu hyvin pienestä otoskoostamme, joka on vain N = 10.
joka tapauksessa tämä on huono uutinen yritys X: lle: älykkyysosamäärä ei sittenkään ennusta kovin kauniisti työsuoritusta.

Regressiooletusten arviointi

regressiooletusten pääoletukset ovat

1. riippumattomat havainnot;
2. normaalius: virheiden on noudatettava normaalijakaumaa populaatiossa;
3. lineaarisuus: kunkin ennustajan ja riippuvan muuttujan välinen suhde on lineaarinen;
4. Homoskedastisuus: virheillä on oltava vakiovarianssi kaikilla ennustetun arvon tasoilla.

1. Jos jokainen tapaus (datanäkymän solujen rivi) SPSS: ssä edustaa erillistä henkilöä, oletamme yleensä, että nämä ovat ”riippumattomia havaintoja”. Seuraavaksi oletukset 2-4 arvioidaan parhaiten tarkastamalla regressioaloitteet tuotoksessamme.

2. Jos normaalius pätee, regressiomme jäännökset on (karkeasti) jaettava normaalisti. Alla oleva histogrammi ei näytä selvää poikkeamaa normaaliudesta.

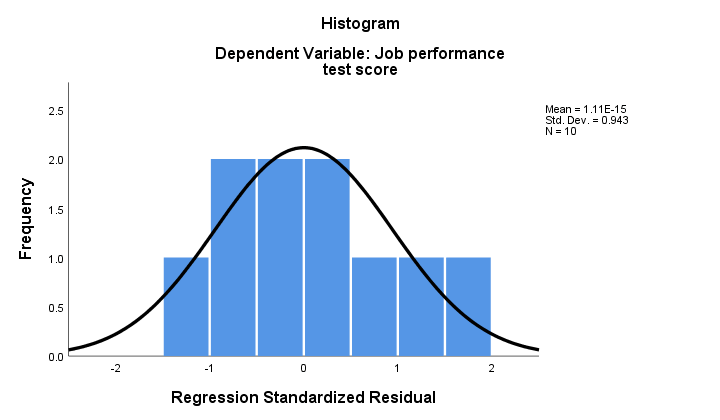
regressiomenettely voi lisätä nämä jäännökset uutena muuttujana tietoihisi. Tekemällä niin, voit ajaa Kolmogorov-Smirnov testi normaalius niitä. Käsillä olevan pienen näytteen osalta tällä testillä tuskin on kuitenkaan tilastollista voimaa. Jätetään se väliin.

The 3. lineaarisuus ja 4. homoskedastisuusoletukset arvioidaan parhaiten jäännöskuviosta. Tämä on scatterplot, jonka ennustetut arvot x-akselilla ja jäännökset y-akselilla kuten alla esitetään. Molemmat muuttujat on standardoitu, mutta tämä ei vaikuta pisteiden kuvion muotoon.

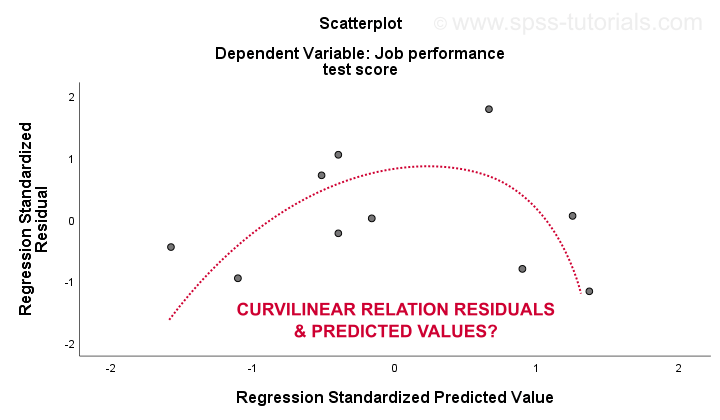
rehellisesti sanottuna jäännöskuvaston käyryys on voimakas. Piirsin käsin käyrän, joka mielestäni sopii parhaiten yleiskaavaan. Olettaen, että käyrä suhde luultavasti ratkaisee heteroscedasticity liian mutta asiat käyvät aivan liian tekninen nyt.Perus pointti on yksinkertaisesti se, että jotkut oletukset eivät pidä.Yleisimmät ratkaisut näihin ongelmiin-huonoimmasta parhaaseen-ovat

• näiden oletusten huomiotta jättäminen kokonaan;
• valehteleminen siitä, että regressioaloitteet eivät osoita mallioletusten rikkomista;
• epälineaarinen muunnos-kuten logaritminen-riippuvaiseksi muuttujaksi;
• sovitus käyrälineaariseen malliin-jonka annamme minuutin kuluttua.

APA Guidelines for Reporting Regression

alla oleva kuva on-aivan kirjaimellisesti – oppikirjan mukainen havainnollistus regression raportoimiseksi APA-muodossa.

tämän tarkan taulukon luominen SPSS-tulosteesta on todellinen riesa. Editointi se menee helpommin Excel kuin WORD niin, että voi säästää ainakin jonkin verran vaivaa.
yritä vaihtoehtoisesti päästä pälkähästä kopioimalla (muokkaamaton) SPSS-ulostulo ja teeskentele tietämätöntä tarkasta APA-muodosta.

ei-lineaarinen Regressiokoe

otoskoko on liian pieni, jotta se sopisi oikeastaan mihinkään lineaarisen mallin ulkopuoliseen. Mutta teimme sen kuitenkin-vain uteliaisuuttamme. Helpoin vaihtoehto SPSS: ssä on Analysis regressio käyrän estimointi.Emme aio keskustella dialogit mutta liitimme syntaksi alla.

SPSS epälineaarinen regressio syntaksi

tulokset

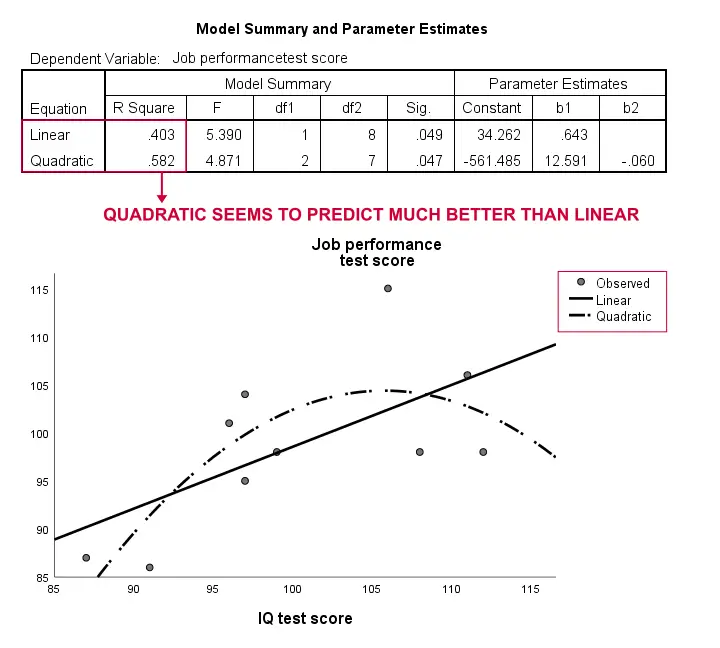
jälleen otoksemme on aivan liian pieni päättelemään mitään vakavaa. Tulokset viittaavat kuitenkin siihen, että kaareva malli sopii dataamme paljon paremmin kuin lineaarinen malli. Emme aio tutkia tätä enempää, mutta halusimme mainita sen; meistä tuntuu, että kurvikkaat mallit ovat rutiininomaisesti huomiotta yhteiskuntatieteilijät.

Kiitos lukemisesta!