Miten löytää korkean kertaluvun johdannaiset
toisen, kolmannen, neljännen tai korkeamman derivaatan löytäminen on uskomattoman yksinkertaista. Funktion toinen derivaatta on vain sen ensimmäisen derivaatan derivaatta. Kolmas derivaatta on toisen derivaatan derivaatta, neljäs derivaatta on kolmannen derivaatta ja niin edelleen.
esimerkiksi tässä on funktio ja sen ensimmäinen, toinen, kolmas ja sitä seuraavat derivaatat. Tässä esimerkissä kaikki derivaatat saadaan potenssisäännöllä:
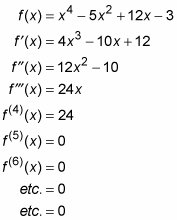
kaikki tämänkaltaiset polynomifunktiot menevät lopulta nollaan, kun eriytyy toistuvasti. Toisaalta rationaalifunktiot kuten
Hanki messier ja messier kun otat enemmän ja enemmän johdannaisia. Sinin ja kosinin korkeammat johdannaiset ovat syklisiä. Esimerkiksi,
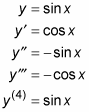
sykli toistuu loputtomasti jokaisella neljän kerrannaisella.
ensimmäinen derivaatta kertoo, kuinka nopeasti funktio muuttuu — Kuinka nopeasti se menee ylös tai alas — se on sen kaltevuus. Toinen derivaatta kertoo, kuinka nopeasti ensimmäinen derivaatta muuttuu-tai toisin sanoen, kuinka nopeasti Rinne muuttuu. Kolmas derivaatta kertoo, kuinka nopeasti toinen derivaatta muuttuu, mikä kertoo, kuinka nopeasti Rinteen muutosvauhti muuttuu.
jos tässä vähän eksyy, ei hätää. On yhä vaikeampaa saada otetta siitä, mitä korkeammat derivaatat kertovat, kun ohitat toisen derivaatan, koska alat päästä muutosnopeuteen ja niin edelleen.




