Tutorial de Regresión Lineal Simple SPSS

Tutorial de Regresión Lineal Simple SPSS

1. Crear Diagrama de dispersión con Línea de ajuste
2. Diálogos de Regresión Lineal SPSS
3. Interpretación de la Salida de Regresión SPSS
4. Evaluación de los Supuestos de Regresión
5. Directrices de la APA para informar Regresión

Pregunta de investigación y datos

La empresa X hizo que 10 empleados tomaran una prueba de coeficiente intelectual y rendimiento laboral. Los datos resultantes, parte de los cuales se muestran a continuación, están en regresión lineal simple.sav.

Lo principal que la empresa X quiere averiguar es que el coeficiente intelectual de isdoes predice el rendimiento laboral? Y si es así, ¿cómo?Responderemos a estas preguntas ejecutando un análisis de regresión lineal simple en SPSS.

Crear gráfica de dispersión con Línea de ajuste

Un excelente punto de partida para nuestro análisis es una gráfica de dispersión. Esto nos dirá si el coeficiente intelectual y las puntuaciones de rendimiento y su relación, si la hay, tienen algún sentido en primer lugar. Crearemos nuestro gráfico a partir de Gráficos Diálogos heredados Dispersión / Punto y, a continuación, seguiremos las capturas de pantalla a continuación.

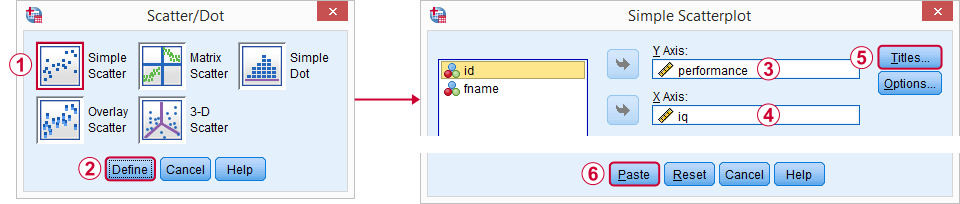
Personalmente me gusta incluir

• un título que dice lo que básicamente está mirando mi audiencia y
• un subtítulo que dice qué encuestados u observaciones se muestran y cuántos.

Recorrer los diálogos resultó en la sintaxis a continuación. Así que vamos a comprobarlo.

Gráfica de dispersión SPSS con sintaxis de títulos

Resultado

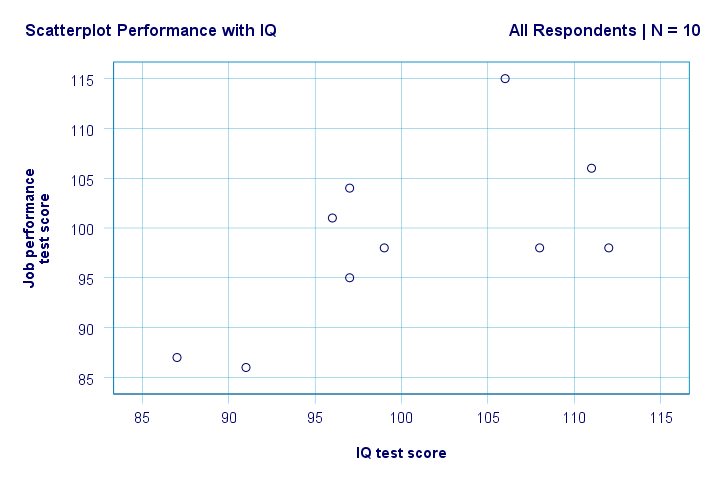
Derecha. En primer lugar, no vemos nada raro en nuestra gráfica de dispersión. Parece haber una correlación moderada entre el coeficiente intelectual y el rendimiento: en promedio, los encuestados con puntajes de CI más altos parecen tener un mejor desempeño. Esta relación parece más o menos lineal.
Ahora agreguemos una línea de regresión a nuestra gráfica de dispersión. Al hacer clic con el botón derecho y seleccionar Editar contenido En una ventana separada, se abre una ventana del Editor de gráficos. Aquí simplemente hacemos clic en el icono «Agregar línea de ajuste al Total», como se muestra a continuación.

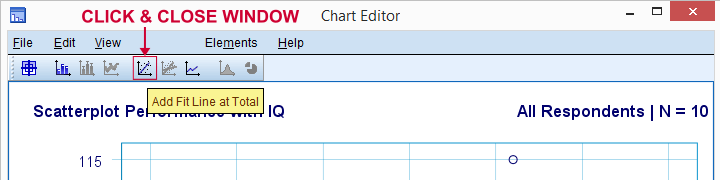
De forma predeterminada, SPSS ahora agrega una línea de regresión lineal a nuestra gráfica de dispersión. El resultado se muestra a continuación.

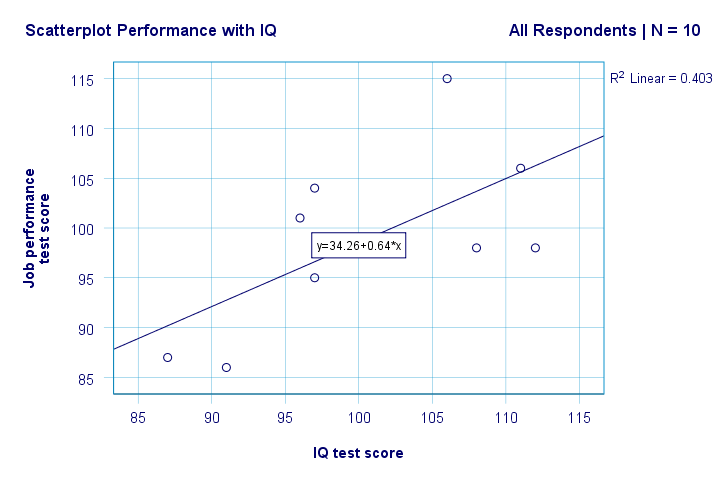
Ahora tenemos algunas primeras respuestas básicas a nuestras preguntas de investigación. R2 = 0,403 indica que el coeficiente intelectual representa alrededor del 40,3% de la varianza en las puntuaciones de rendimiento. Es decir, el coeficiente intelectual predice el rendimiento bastante bien en esta muestra.
Pero, ¿cómo podemos predecir mejor el rendimiento laboral a partir del coeficiente intelectual? Bueno, en nuestra gráfica de dispersión y es el rendimiento (que se muestra en el eje y) y x es el coeficiente intelectual (que se muestra en el eje x). Así que será rendimiento = 34.26 + 0.64 * IQ.So para un solicitante de empleo con un coeficiente intelectual de 115, predeciremos 34.26 + 0.64 * 115 = 107.86 como su puntuación de rendimiento más probable en el futuro.
Correcto, por lo que nos da una idea básica sobre la relación entre el coeficiente intelectual y el rendimiento y la presenta visualmente. Sin embargo, todavía falta mucha información (significancia estadística e intervalos de confianza). Así que vamos a buscarlo.

Diálogos de regresión lineal SPSS

Volver a ejecutar nuestro análisis de regresión mínima desde Analizar Regresión Lineal nos da una salida mucho más detallada. Las capturas de pantalla a continuación muestran cómo procederemos.

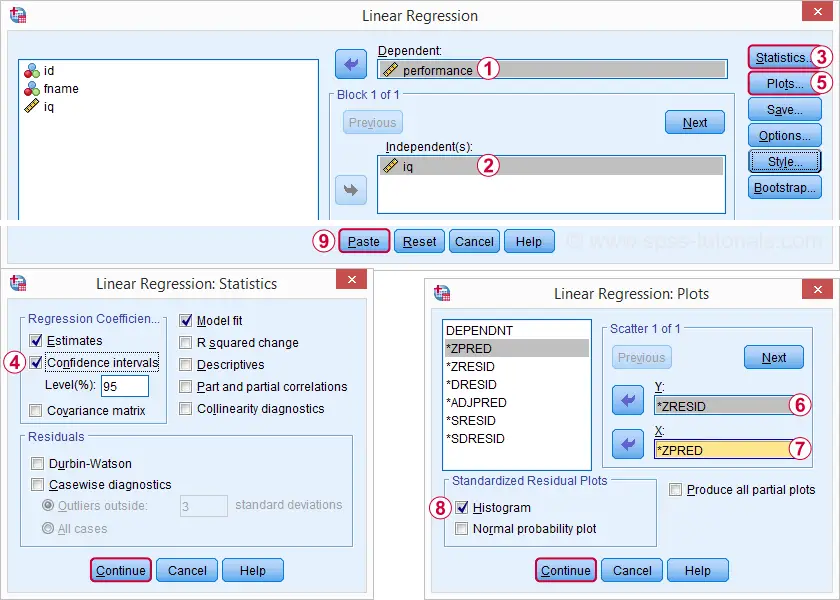
Al seleccionar estas opciones, se muestra la sintaxis a continuación. Vamos a comprobarlo.

Sintaxis de Regresión Lineal Simple SPSS

Coeficientes I de salida de regresión SPSS

Desafortunadamente, SPSS nos da mucha más salida de regresión de la que necesitamos. Podemos ignorar la mayor parte con seguridad. Sin embargo, una tabla de gran importancia es la tabla de coeficientes que se muestra a continuación.

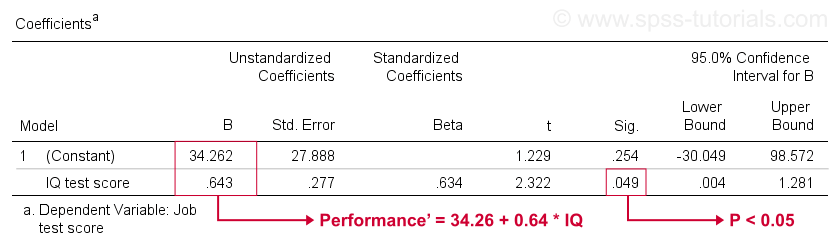
Esta tabla muestra los coeficientes B que ya vimos en nuestra gráfica de dispersión. Como se indicó, estos implican la ecuación de regresión lineal que mejor estima el desempeño laboral a partir del coeficiente intelectual de nuestra muestra.
En segundo lugar, recuerde que generalmente rechazamos la hipótesis nula si p < 0.05. El coeficiente B para el coeficiente intelectual tiene «Sig» o p = 0,049. Es estadísticamente significativamente diferente de cero.
Sin embargo, su intervalo de confianza del 95%- aproximadamente, un rango probable para su valor poblacional – es . Así que B probablemente no es cero, pero bien puede estar muy cerca de cero. El intervalo de confianza es enorme-nuestra estimación para B no es precisa en absoluto – y esto se debe al tamaño de muestra mínimo en el que se basa el análisis.

SPSS Regresión Output II-Resumen del modelo

Además de la tabla de coeficientes, también necesitamos la tabla de Resumen del Modelo para informar nuestros resultados.

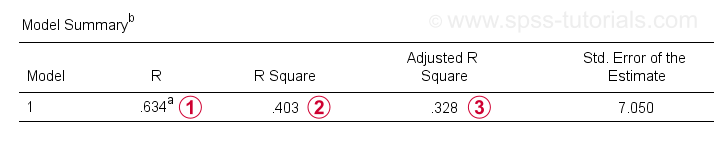
R es la correlación entre los valores predichos de regresión y los valores reales. Para regresión simple, R es igual a la correlación entre el predictor y la variable dependiente.
R Cuadrado – la correlación cuadrada-indica la proporción de varianza en la variable dependiente que representa el predictor(es) en nuestros datos de muestra.
Estimaciones ajustadas de R-cuadrado al aplicar nuestra ecuación de regresión (basada en muestras) a toda la población.
r-cuadrado ajustado proporciona una estimación más realista de la precisión predictiva que simplemente r-cuadrado. En nuestro ejemplo, la gran diferencia entre ellos, generalmente conocida como contracción, se debe a nuestro tamaño de muestra muy mínimo de solo N = 10.
En cualquier caso, estas son malas noticias para la compañía X: IQ no predice el rendimiento laboral tan bien después de todo.

Evaluación de las hipótesis de regresión

Las principales hipótesis de regresión son

1. Observaciones independientes;
2. Normalidad: los errores deben seguir una distribución normal en la población;
3. Linealidad: la relación entre cada predictor y la variable dependiente es lineal;
4. Homocedasticidad: los errores deben tener varianza constante sobre todos los niveles de valor predicho.

1. Si cada caso (fila de celdas en la vista de datos) en SPSS representa a una persona separada, generalmente asumimos que se trata de «observaciones independientes». A continuación, las suposiciones 2-4 se evalúan mejor inspeccionando las gráficas de regresión en nuestra salida.

2. Si la normalidad se mantiene, entonces nuestros residuos de regresión deberían estar (aproximadamente) distribuidos normalmente. El histograma a continuación no muestra una clara desviación de la normalidad.

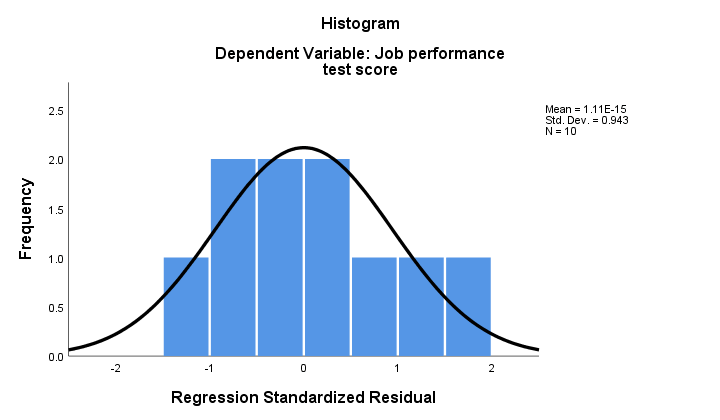
El procedimiento de regresión puede agregar estos residuos como una nueva variable a sus datos. Al hacerlo, podría realizar una prueba de normalidad de Kolmogorov-Smirnov en ellos. Sin embargo, para la pequeña muestra a mano, esta prueba apenas tendrá ningún poder estadístico. Así que saltémonos eso.

El 3. linealidad y 4. las suposiciones de homocedasticidad se evalúan mejor a partir de una parcela residual. Esta es una gráfica de dispersión con valores predichos en el eje x y residuos en el eje y como se muestra a continuación. Ambas variables han sido estandarizadas, pero esto no afecta la forma del patrón de puntos.

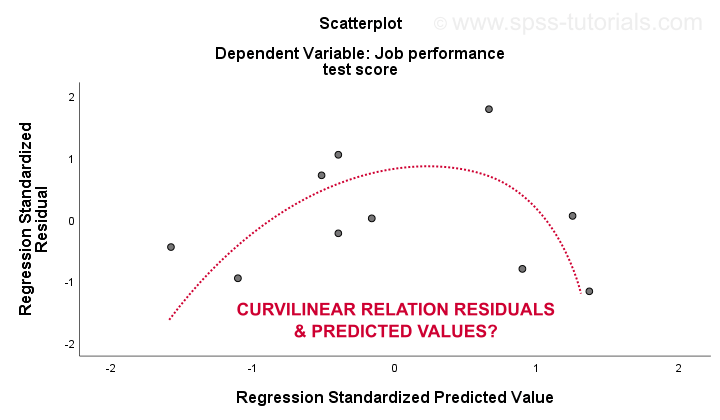
Honestamente, la gráfica residual muestra una curvilinealidad fuerte. Dibujé manualmente la curva que creo que se ajusta mejor al patrón general. Asumir una relación curvilínea probablemente resuelve la heterocedasticidad también, pero las cosas se están volviendo demasiado técnicas ahora.El punto básico es simplemente que algunas suposiciones no se sostienen.Las soluciones más comunes para estos problemas, de lo peor a lo mejor, son

• ignorar por completo estas suposiciones;
• mentir que las gráficas de regresión no indican ninguna violación de las suposiciones del modelo;
• una transformación no lineal, como logarítmica, a la variable dependiente;
• ajustar un modelo curvilíneo, que daremos una oportunidad en un minuto.

Pautas de APA para reportar regresión

La siguiente figura es, literalmente, una ilustración de libro de texto para reportar regresión en formato APA.

Crear esta tabla exacta a partir de la salida de SPSS es un verdadero dolor de cabeza. Editarlo es más fácil en Excel que en WORD, por lo que puede ahorrarle al menos algunos problemas.
Alternativamente, intente copiar y pegar la salida SPSS (sin editar) y fingir que no conoce el formato APA exacto.

Experimento de regresión no lineal

Nuestro tamaño de muestra es demasiado pequeño para adaptarse realmente a cualquier cosa más allá de un modelo lineal. Pero lo hicimos de todos modos, solo curiosidad. La opción más fácil en SPSS está en Analizar Regresión Estimación de curvas.No vamos a discutir los diálogos, pero pegamos la sintaxis a continuación.

Sintaxis de Regresión No Lineal SPSS

Resultados

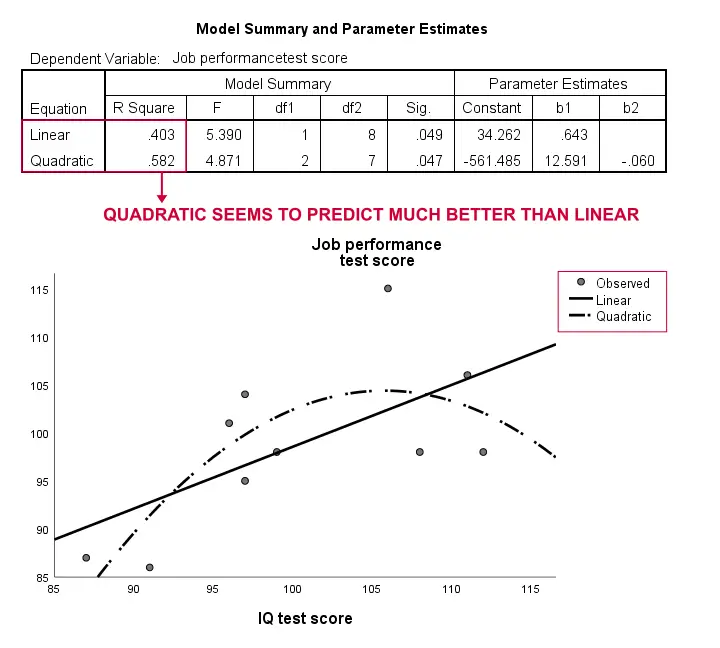
De nuevo, nuestra muestra es demasiado pequeña para concluir algo serio. Sin embargo, los resultados sugieren un poco que un modelo curvilíneo se ajusta a nuestros datos mucho mejor que el lineal. No exploraremos esto más, pero queríamos mencionarlo; sentimos que los modelos curvilíneos son ignorados rutinariamente por los científicos sociales.

Gracias por leer!