Cómo Encontrar Derivados de Alto Orden
Encontrar una segunda, tercera, cuarta o mayor derivada es increíblemente simple. La segunda derivada de una función es la derivada de su primera derivada. La tercera derivada es la derivada de la segunda derivada, la cuarta derivada es la derivada de la tercera, y así sucesivamente.
Por ejemplo, aquí está una función y sus derivadas primera, segunda, tercera y posteriores. En este ejemplo, todas las derivadas se obtienen mediante la regla de potencia:
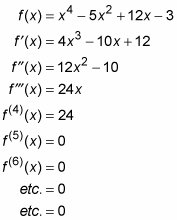
Todas las funciones polinómicas como esta eventualmente van a cero cuando se diferencian repetidamente. Por otro lado, funciones racionales como
se vuelve más y más desordenado a medida que toma derivados más y más altos. Y las derivadas más altas de seno y coseno son cíclicas. Por ejemplo,
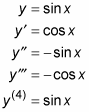
El ciclo se repite indefinidamente con cada múltiplo de cuatro.
Una primera derivada te dice qué tan rápido está cambiando una función, qué tan rápido va hacia arriba o hacia abajo, esa es su pendiente. Una segunda derivada te dice qué tan rápido está cambiando la primera derivada — o, en otras palabras, qué tan rápido está cambiando la pendiente. Una tercera derivada te dice qué tan rápido está cambiando la segunda derivada, que te dice qué tan rápido está cambiando la tasa de cambio de la pendiente.
Si te estás perdiendo un poco, no te preocupes. Se vuelve cada vez más difícil entender qué derivados más altos le dicen a medida que pasa por la segunda derivada, porque comienza a entrar en una tasa de cambio de una tasa de cambio de una tasa de cambio, y así sucesivamente.




