SPSS Einfache lineare Regression Tutorial

SPSS Einfache lineare Regression Tutorial

1. Streudiagramm mit Anpassungslinie erstellen
2. SPSS Lineare Regressionsdialoge
3. SPSS-Regressionsausgabe interpretieren
4. Bewertung der Regressionsannahmen
5. APA-Richtlinien für die Berichterstattung über Regression

Forschungsfrage und Daten

Unternehmen X ließ 10 Mitarbeiter einen IQ- und Arbeitsleistungstest machen. Die resultierenden Daten – von denen ein Teil unten gezeigt wird – sind in einfacher-linearer-Regression.sav.

Die Hauptsache, die Unternehmen X herausfinden möchte, istsagt IQ die Arbeitsleistung voraus? Und -wenn ja – wie?Wir beantworten diese Fragen, indem wir eine einfache lineare Regressionsanalyse in SPSS ausführen.

Streudiagramm mit Anpassungslinie erstellen

Ein guter Ausgangspunkt für unsere Analyse ist ein Streudiagramm. Dies wird uns sagen, ob die IQ- und Leistungswerte und ihre Beziehung – falls vorhanden – überhaupt Sinn machen. Wir erstellen unser Diagramm aus Graphen Legacy-Dialogen Scatter / Dot und folgen dann den folgenden Screenshots.

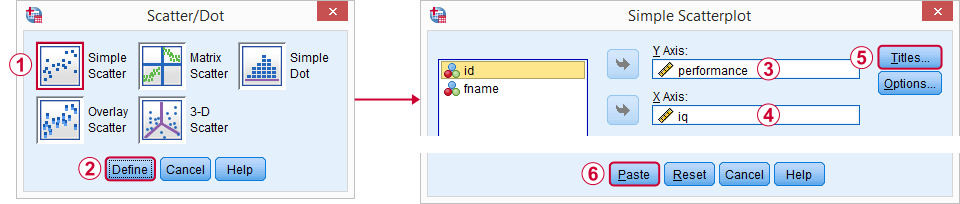
Ich persönlich mag es zu werfen

• ein Titel, der angibt, was mein Publikum im Grunde betrachtet, und
• ein Untertitel, der angibt, welche Befragten oder Beobachtungen angezeigt werden und wie viele.

Das Durchlaufen der Dialoge führte zu der folgenden Syntax. Also lass es uns laufen.

SPSS-Streudiagramm mit Titelsyntax

Ergebnis

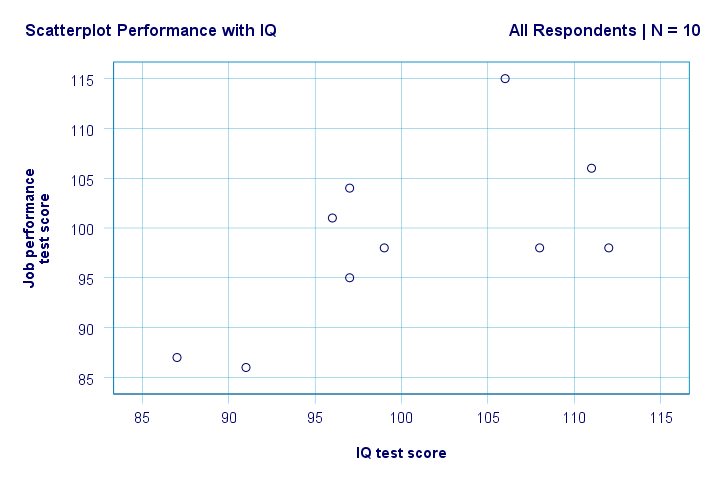
Rechts. Zunächst einmal sehen wir in unserem Streudiagramm nichts Seltsames. Es scheint eine moderate Korrelation zwischen IQ und Leistung zu geben: im Durchschnitt scheinen Befragte mit höheren IQ-Werten eine bessere Leistung zu erbringen. Diese Beziehung sieht ungefähr linear aus.
Fügen wir nun eine Regressionsgerade zu unserem Streudiagramm hinzu. Wenn Sie mit der rechten Maustaste darauf klicken und Inhalt bearbeiten In einem separaten Fenster auswählen, wird ein Diagrammeditorfenster geöffnet. Hier klicken wir einfach auf das Symbol „Fit Line at Total hinzufügen“, wie unten gezeigt.

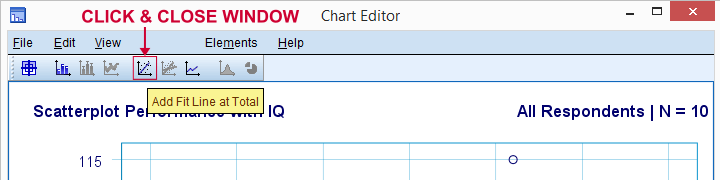
Standardmäßig fügt SPSS unserem Streudiagramm jetzt eine lineare Regressionslinie hinzu. Das Ergebnis ist unten dargestellt.

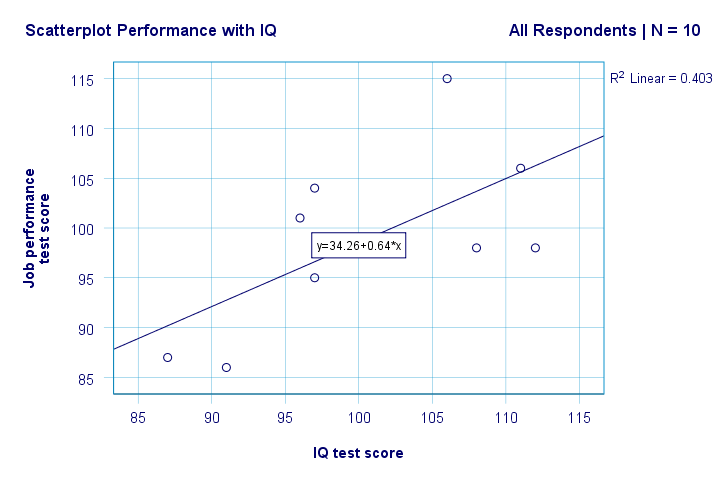
Wir haben nun einige erste grundlegende Antworten auf unsere Forschungsfragen. R2 = 0,403 zeigt an, dass der IQ etwa 40,3% der Varianz der Leistungswerte ausmacht. Das heißt, IQ prognostiziert die Leistung in dieser Stichprobe ziemlich gut.
Aber wie können wir die Arbeitsleistung am besten anhand des IQ vorhersagen? Nun, in unserem Streudiagramm ist y die Leistung (auf der y-Achse gezeigt) und x ist IQ (auf der x-Achse gezeigt). Das wird also Leistung = 34,26 + 0,64 * IQ.So für einen Bewerber mit einem IQ von 115 sagen wir Folgendes voraus 34.26 + 0.64 * 115 = 107.86 als seine / ihre wahrscheinlichste zukünftige Performance-Score.
Richtig, das gibt uns eine grundlegende Vorstellung über die Beziehung zwischen IQ und Leistung und stellt sie visuell dar. Es fehlen jedoch noch viele Informationen – statistische Signifikanz und Konfidenzintervalle. Also lass es uns holen.

SPSS Lineare Regressionsdialoge

Das erneute Ausführen unserer minimalen Regressionsanalyse von Analyze Regression Linear gibt uns eine viel detailliertere Ausgabe. Die Screenshots unten zeigen, wie wir vorgehen werden.

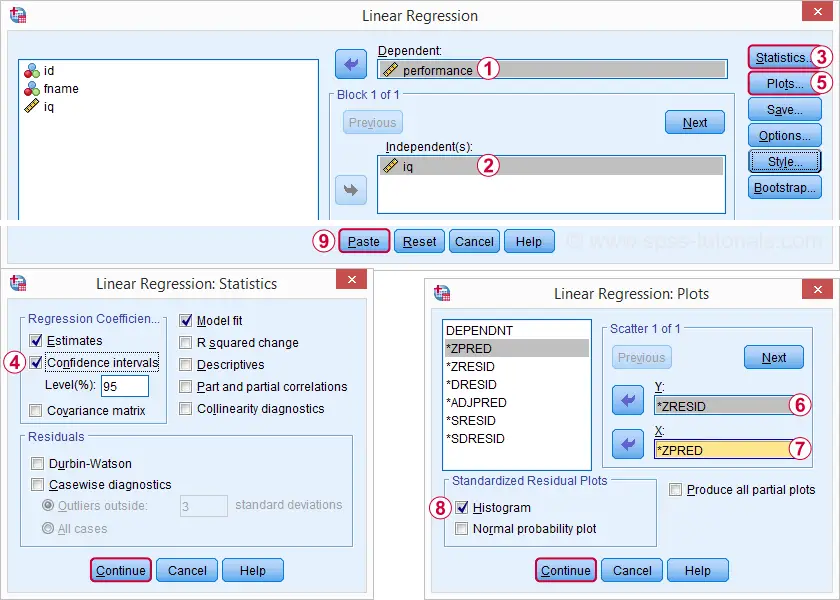
Wenn Sie diese Optionen auswählen, wird die folgende Syntax angezeigt. Lass es uns laufen.

SPSS Einfache lineare Regressionssyntax

SPSS-Regressionsausgabe I – Koeffizienten

Leider liefert uns SPSS viel mehr Regressionsausgabe, als wir benötigen. Wir können das meiste sicher ignorieren. Eine Tabelle von großer Bedeutung ist jedoch die unten gezeigte Koeffiziententabelle.

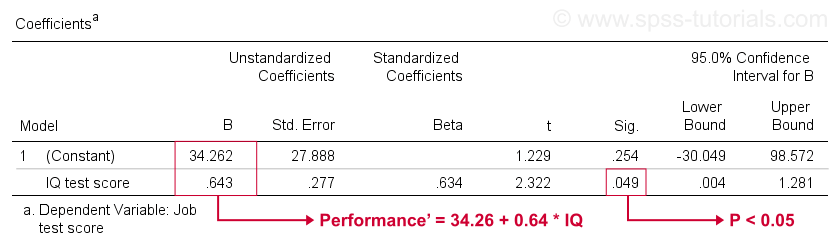
Diese Tabelle zeigt die B-Koeffizienten, die wir bereits in unserem Streudiagramm gesehen haben. Wie bereits erwähnt, implizieren diese die lineare Regressionsgleichung, die die Arbeitsleistung am besten anhand des IQ in unserer Stichprobe abschätzt.
Zweitens, denken Sie daran, dass wir normalerweise die Nullhypothese ablehnen, wenn p < 0,05. Der B-Koeffizient für IQ hat „Sig“ oder p = 0,049. Es ist statistisch signifikant verschieden von Null.
Sein 95% -Konfidenzintervall – ungefähr ein wahrscheinlicher Bereich für seinen Populationswert – ist jedoch . B ist also wahrscheinlich nicht Null, aber es kann sehr nahe an Null liegen. Das Konfidenzintervall ist enorm – unsere Schätzung für B ist überhaupt nicht präzise – und dies liegt an der minimalen Stichprobengröße, auf der die Analyse basiert.

SPSS-Regressionsausgabe II – Modellübersicht

Neben der Koeffiziententabelle benötigen wir auch die Modellübersicht, um unsere Ergebnisse zu melden.

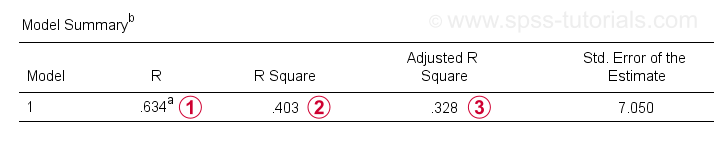
R ist die Korrelation zwischen den vorhergesagten Werten der Regression und den tatsächlichen Werten. Bei der einfachen Regression ist R gleich der Korrelation zwischen Prädiktor und abhängiger Variable.
Das Quadrat – die quadratische Korrelation – gibt den Anteil der Varianz in der abhängigen Variablen an, der von den Prädiktoren in unseren Beispieldaten berücksichtigt wird.
Das bereinigte R-Quadrat schätzt das R-Quadrat, wenn unsere (stichprobenbasierte) Regressionsgleichung auf die gesamte Grundgesamtheit angewendet wird.
Das bereinigte R-Quadrat liefert eine realistischere Schätzung der Vorhersagegenauigkeit als das einfache r-Quadrat. In unserem Beispiel ist der große Unterschied zwischen ihnen – allgemein als Schrumpfung bezeichnet – auf unsere sehr minimale Stichprobengröße von nur N = 10 zurückzuführen.
In jedem Fall ist dies eine schlechte Nachricht für Unternehmen X: IQ prognostiziert die Arbeitsleistung nicht wirklich so gut.

Bewertung der Regressionsannahmen

Die Hauptannahmen für die Regression sind

1. Unabhängige Beobachtungen;
2. Normalität: Fehler müssen einer Normalverteilung in der Grundgesamtheit folgen;
3. Linearität: Die Beziehung zwischen jedem Prädiktor und der abhängigen Variablen ist linear;
4. Homoskedastizität: Fehler müssen eine konstante Varianz über alle Ebenen des vorhergesagten Werts aufweisen.

1. Wenn jeder Fall (Zellenzeile in der Datenansicht) in SPSS eine separate Person darstellt, gehen wir normalerweise davon aus, dass es sich um „unabhängige Beobachtungen“ handelt. Als nächstes werden die Annahmen 2-4 am besten bewertet, indem die Regressionsdiagramme in unserer Ausgabe überprüft werden.

2. Wenn die Normalität gilt, sollten unsere Regressionsresiduen (ungefähr) normal verteilt sein. Das Histogramm unten zeigt keine klare Abweichung von der Normalität.

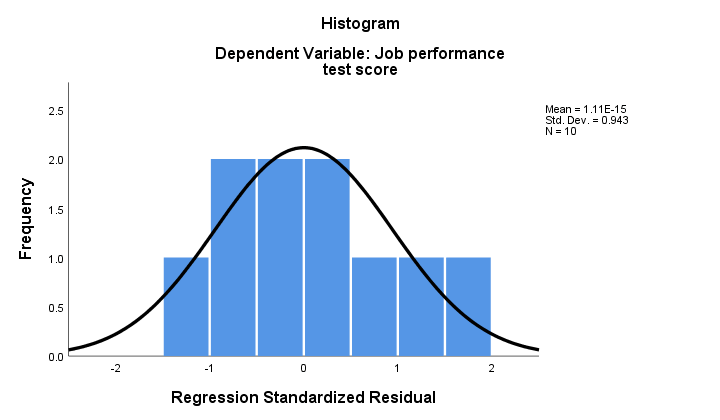
Das Regressionsverfahren kann diese Residuen als neue Variable zu Ihren Daten hinzufügen. Auf diese Weise könnten Sie einen Kolmogorov-Smirnov-Test auf Normalität durchführen. Für die winzige Stichprobe wird dieser Test jedoch kaum statistische Aussagekraft haben. Also lass es uns überspringen.

Die 3. linearität und 4. Homoskedastizitätsannahmen werden am besten anhand eines Residuendiagramms bewertet. Dies ist ein Streudiagramm mit vorhergesagten Werten in der x-Achse und Residuen auf der y-Achse, wie unten gezeigt. Beide Variablen wurden standardisiert, dies hat jedoch keinen Einfluss auf die Form des Punktmusters.

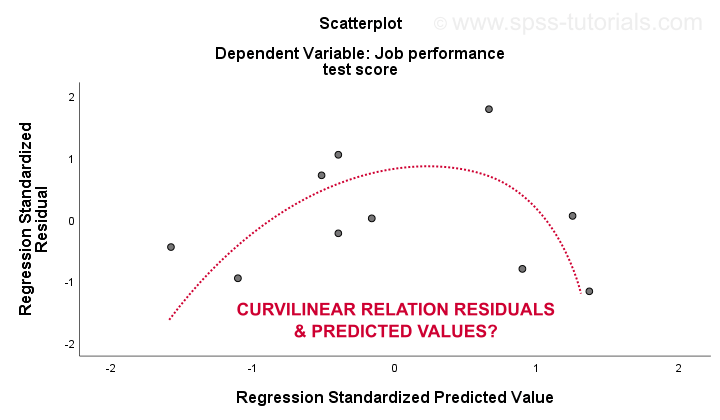
Ehrlich gesagt zeigt das Residuendiagramm eine starke Krummlinearität. Ich habe manuell die Kurve gezeichnet, die meiner Meinung nach am besten zum Gesamtmuster passt. Die Annahme einer krummlinigen Beziehung löst wahrscheinlich auch die Heteroskedastizität auf, aber die Dinge werden jetzt viel zu technisch.Der grundlegende Punkt ist einfach, dass einige Annahmen nicht gelten.Die häufigsten Lösungen für diese Probleme – vom schlechtesten zum besten – sind

• Ignorieren dieser Annahmen insgesamt;
• Lügen, dass die Regressionsdiagramme keine Verstöße gegen die Modellannahmen anzeigen;
• eine nichtlineare Transformation – wie logarithmisch – zur abhängigen Variablen;
• Anpassung eines krummlinigen Modells – das wir in einer Minute ausprobieren werden.

APA-Richtlinien für die Berichterstattung über Regression

Die folgende Abbildung ist – im wahrsten Sinne des Wortes – eine Lehrbuchillustration für die Berichterstattung über Regression im APA-Format.

Das Erstellen dieser genauen Tabelle aus der SPSS-Ausgabe ist ein echter Schmerz im Arsch. Das Bearbeiten ist in Excel einfacher als in WORD, sodass Sie möglicherweise einige Probleme haben.
Versuchen Sie alternativ, die (unbearbeitete) SPSS-Ausgabe durch Kopieren und Einfügen zu entfernen, und geben Sie vor, das genaue APA-Format nicht zu kennen.

Nichtlineares Regressionsexperiment

Unsere Stichprobengröße ist zu klein, um wirklich etwas über ein lineares Modell hinaus zu passen. Aber wir haben es trotzdem getan – nur Neugier. Die einfachste Option in SPSS ist unter Analysieren Regression Kurvenschätzung.Wir werden die Dialoge nicht diskutieren, aber wir haben die folgende Syntax eingefügt.

SPSS Nichtlineare Regressionssyntax

Ergebnisse

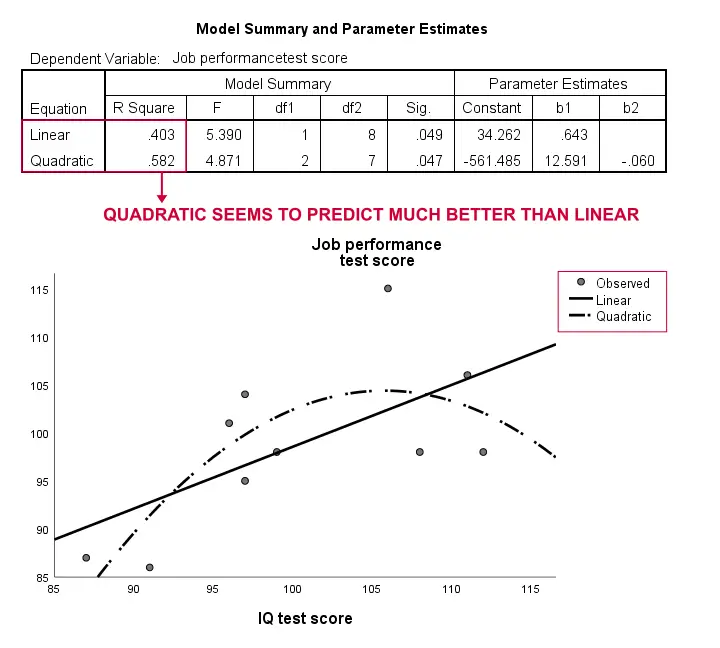
Auch hier ist unsere Stichprobe viel zu klein, um auf etwas Ernstes schließen zu können. Die Ergebnisse deuten jedoch darauf hin, dass ein krummliniges Modell viel besser zu unseren Daten passt als das lineare. Wir werden dies nicht weiter untersuchen, aber wir wollten es erwähnen; Wir sind der Meinung, dass krummlinige Modelle von Sozialwissenschaftlern routinemäßig übersehen werden.

Danke fürs Lesen!