So finden Sie Derivate höherer Ordnung
Das Finden einer zweiten, dritten, vierten oder höheren Ableitung ist unglaublich einfach. Die zweite Ableitung einer Funktion ist nur die Ableitung ihrer ersten Ableitung. Die dritte Ableitung ist die Ableitung der zweiten Ableitung, die vierte Ableitung ist die Ableitung der dritten und so weiter.
Hier ist beispielsweise eine Funktion und ihre erste, zweite, dritte und nachfolgende Ableitung. In diesem Beispiel werden alle Ableitungen durch die Potenzregel erhalten:
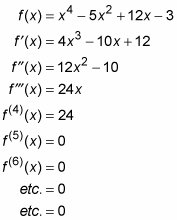
Alle Polynomfunktionen wie diese gehen schließlich auf Null, wenn Sie wiederholt differenzieren. Rationale Funktionen wie
erhalten Sie unordentlicher und unordentlicher, während Sie höhere und höhere Ableitungen nehmen. Und die höheren Ableitungen von Sinus und Cosinus sind zyklisch. Zum Beispiel,
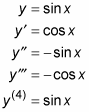
Der Zyklus wiederholt sich unbegrenzt mit jedem Vielfachen von vier.
Eine erste Ableitung sagt Ihnen, wie schnell sich eine Funktion ändert — wie schnell sie auf- oder absteigt — das ist ihre Steigung. Eine zweite Ableitung gibt an, wie schnell sich die erste Ableitung ändert — oder mit anderen Worten, wie schnell sich die Steigung ändert. Eine dritte Ableitung gibt an, wie schnell sich die zweite Ableitung ändert, die angibt, wie schnell sich die Änderungsrate der Steigung ändert.
Wenn Sie sich hier ein bisschen verirren, machen Sie sich keine Sorgen. Es wird immer schwieriger, in den Griff zu bekommen, was höhere Derivate Ihnen sagen, wenn Sie an der zweiten Ableitung vorbeigehen, weil Sie anfangen, in eine Änderungsrate einer Änderungsrate einer Änderungsrate usw. zu geraten.




