SPSS Simple lineær Regression Tutorial
- Opret Scatterplot med Fit Line
- SPSS lineær Regression dialoger
- tolkning SPSS Regression Output
- evaluering af Regressionsforudsætninger
- APA retningslinjer for rapportering Regression
forskningsspørgsmål og data
virksomheden fik 10 ansatte til at tage en IK-og Jobpræstationstest. De resulterende data-hvoraf en del er vist nedenfor – er i enkel-lineær regression.sav.
det vigtigste firma ønsker at finde ud af isforudsiger ik jobpræstation? Og-hvis ja-hvordan?Vi besvarer disse spørgsmål ved at køre en simpel lineær regressionsanalyse i SPSS.
Opret Scatterplot med Fit Line
et godt udgangspunkt for vores Analyse er en scatterplot. Dette vil fortælle os, om IK og præstationsresultater og deres forhold-hvis nogen – giver mening i første omgang. Vi opretter vores diagram ud fra grafer  Ældre dialoger
Ældre dialoger  Scatter/Dot, og vi følger derefter skærmbillederne nedenfor.
Scatter/Dot, og vi følger derefter skærmbillederne nedenfor.
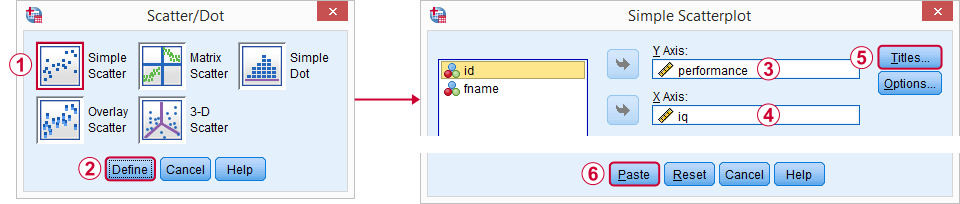
 jeg personligt gerne smide i
jeg personligt gerne smide i
- en titel, der siger, hvad mit publikum dybest set ser på, og
- en undertekst, der siger, hvilke respondenter eller observationer der vises, og hvor mange.
at gå gennem dialogerne resulterede i syntaksen nedenfor. Så lad os køre det.
SPSS Scatterplot med titler syntaks
graf
/SCATTERPLOT(BIVAR)=IK med performance
/mangler=LISTEVIS
/TITLE=’Scatterplot Performance med IK’
/undertekst ‘alle respondenter | N = 10’.
resultat
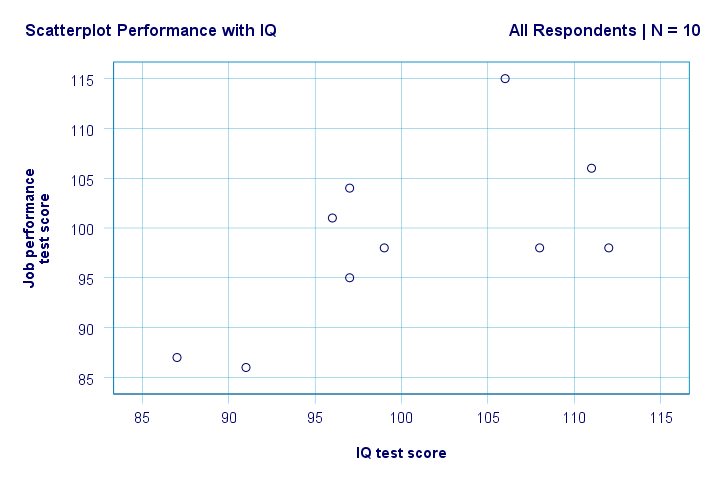
højre. Så for det første ser vi ikke noget underligt i vores scatterplot. Der synes at være en moderat sammenhæng mellem IK og ydeevne: i gennemsnit synes respondenter med højere ik-score at klare sig bedre. Dette forhold ser nogenlunde lineært ud.
lad os nu tilføje en regressionslinje til vores scatterplot. Højreklik på det og vælg Rediger indhold  i separat vindue åbner et Diagramredigeringsvindue. Her klikker vi blot på ikonet “Tilføj Fit Line at Total” som vist nedenfor.
i separat vindue åbner et Diagramredigeringsvindue. Her klikker vi blot på ikonet “Tilføj Fit Line at Total” som vist nedenfor.
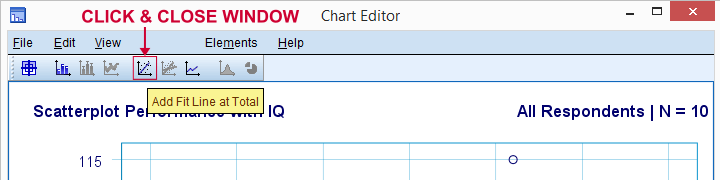
som standard tilføjer SPSS nu en lineær regressionslinje til vores scatterplot. Resultatet er vist nedenfor.
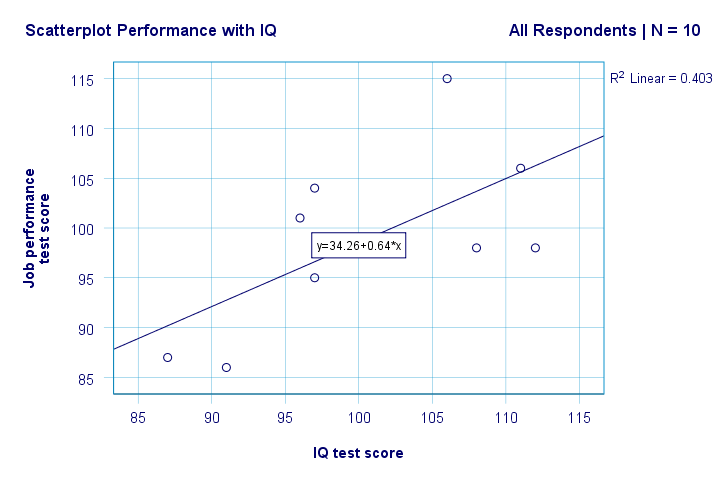
vi har nu nogle første grundlæggende svar på vores forskningsspørgsmål. R2 = 0,403 angiver, at IK tegner sig for omkring 40,3% af variansen i præstationsresultater. Det vil sige, at IK forudsiger ydeevne ret godt i denne prøve.
men hvordan kan vi bedst forudsige jobpræstationer fra IK? Nå, i vores scatterplot y er ydeevne (vist på y-aksen) og K er ik (vist på h-aksen). Så det vil beperformance = 34.26 + 0.64 * IQ.So for en jobansøger med en ik-score på 115 forudsiger vi 34.26 + 0.64 * 115 = 107.86 som hans / hendes mest sandsynlige fremtidige præstationsscore.
højre, så det giver os en grundlæggende ide om forholdet mellem IK og ydeevne og præsenterer det visuelt. Imidlertid mangler der stadig meget information-statistisk signifikans og konfidensintervaller. Så lad os tage den.
SPSS lineære Regressionsdialoger
Genkørsel af vores minimale regressionsanalyse fra analyse Regression
Regression lineær giver os meget mere detaljeret output. Skærmbillederne nedenfor viser, hvordan vi fortsætter.
lineær giver os meget mere detaljeret output. Skærmbillederne nedenfor viser, hvordan vi fortsætter.
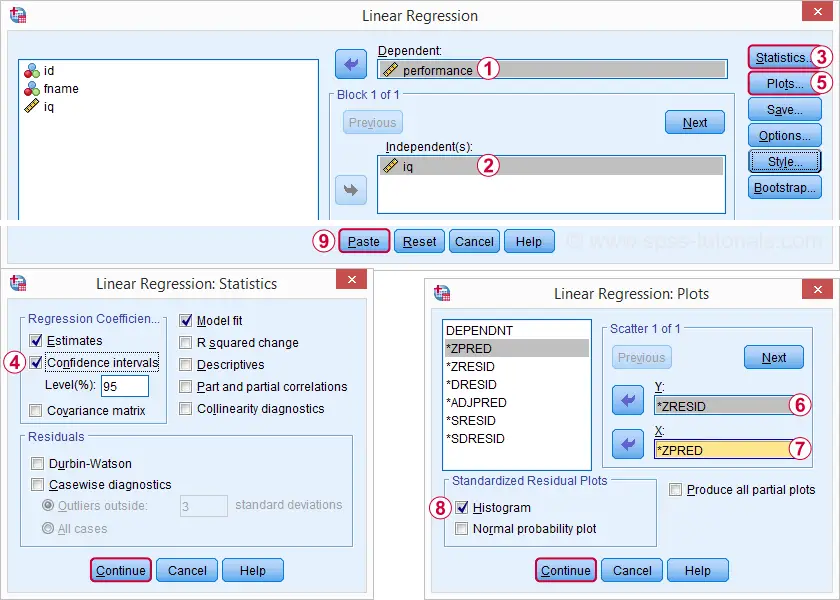
valg af disse indstillinger resulterer i syntaksen nedenfor. Lad os køre det.
SPSS simpel lineær Regressionssyntaks
REGRESSION
/MANGLER LISTEVIS
/STATISTIK COEFF OUTS CI(95) R ANOVA
/KRITERIER=PIN(.05)trut (.10)
/NOORIGIN
/afhængig ydelse
/metode=indtast ik
/SCATTERPLOT=(*RRESID ,*RPRED)
/rester HISTOGRAM(RRESID).
SPSS Regressionsudgang I – koefficienter
desværre giver SPSS os meget mere regressionsudgang, end vi har brug for. Vi kan sikkert ignorere det meste af det. En tabel af stor betydning er imidlertid koefficienttabellen vist nedenfor.
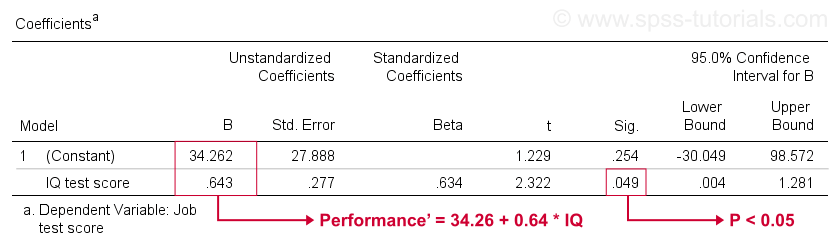
denne tabel viser de B-koefficienter, vi allerede så i vores scatterplot. Som angivet indebærer disse den lineære regressionsligning, der bedst estimerer jobpræstation ud fra IK i vores prøve.
for det andet skal du huske, at vi normalt afviser nulhypotesen, hvis p < 0,05. B-koefficienten for IK har “Sig” eller p = 0,049. Det er statistisk signifikant forskelligt fra nul.
men dens 95% konfidensinterval-omtrent et sandsynligt interval for dets befolkningsværdi – er . Så B er sandsynligvis ikke nul, men det kan godt være meget tæt på nul. Konfidensintervallet er enormt-vores estimat for B er slet ikke præcist – og dette skyldes den minimale stikprøvestørrelse, som analysen er baseret på.
SPSS Regressionsudgang II – modeloversigt
bortset fra koefficienttabellen har vi også brug for Modeloversigtstabellen til rapportering af vores resultater.
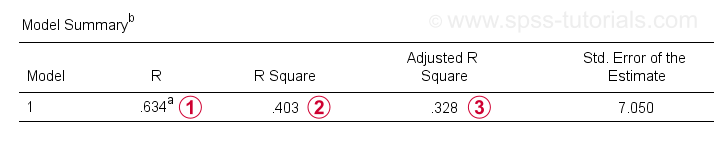
 R er sammenhængen mellem de forudsagte regressionsværdier og de faktiske værdier. For simpel regression er R lig med korrelationen mellem forudsigeren og den afhængige variabel.
R er sammenhængen mellem de forudsagte regressionsværdier og de faktiske værdier. For simpel regression er R lig med korrelationen mellem forudsigeren og den afhængige variabel.
 R kvadrat-den kvadratiske korrelation – angiver andelen af varians i den afhængige variabel, der regnes med forudsigeren(e) i vores eksempeldata.
R kvadrat-den kvadratiske korrelation – angiver andelen af varians i den afhængige variabel, der regnes med forudsigeren(e) i vores eksempeldata.
 justerede R-kvadrat estimater R-kvadrat, når vi anvender vores (prøvebaserede) regressionsligning på hele befolkningen.
justerede R-kvadrat estimater R-kvadrat, når vi anvender vores (prøvebaserede) regressionsligning på hele befolkningen.
justeret r-firkant giver et mere realistisk skøn over forudsigelig nøjagtighed end blot r-firkant. I vores eksempel skyldes den store forskel mellem dem – generelt benævnt krympning-vores meget minimale prøvestørrelse på kun N = 10.
under alle omstændigheder er dette dårlige nyheder for virksomheden: ik forudsiger ikke rigtig jobpræstationer så pænt.
evaluering af Regressionsforudsætninger
de vigtigste antagelser for regression er
- uafhængige observationer;
- normalitet: fejl skal følge en normal fordeling i befolkningen;
- linearitet: forholdet mellem hver forudsigelse og den afhængige variabel er lineær;
- Homoscedasticity: fejl skal have konstant varians over alle niveauer af forudsagt værdi.
1. Hvis hvert tilfælde (række af celler i datavisning) i SPSS repræsenterer en separat person, antager vi normalt, at dette er “uafhængige observationer”. Dernæst vurderes antagelser 2-4 bedst ved at inspicere regressionsplotterne i vores output.
2. Hvis normaliteten holder, skal vores regressionsrester (groft) fordeles normalt. Histogrammet nedenfor viser ikke en klar afvigelse fra normalitet.
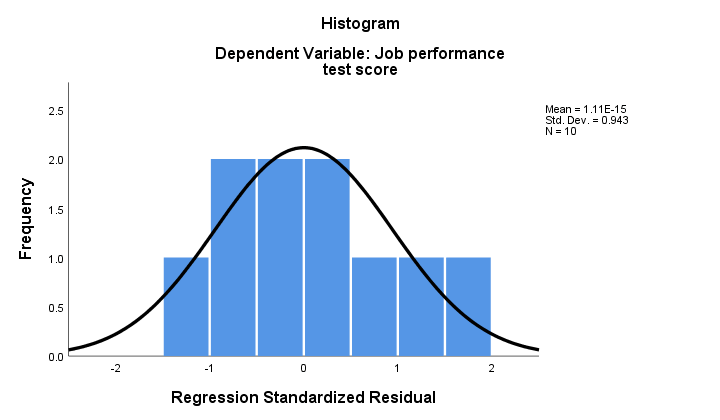
regressionsproceduren kan tilføje disse rester som en ny variabel til dine data. Ved at gøre det kunne du køre en Kolmogorov-Smirnov-test for normalitet på dem. For den lille prøve ved hånden vil denne test imidlertid næppe have nogen statistisk styrke. Så lad os springe det over.
den 3. linearitet og 4. homoscedasticity antagelser vurderes bedst ud fra et resterende plot. Dette er en scatterplot med forudsagte værdier i h-aksen og rester på y-aksen som vist nedenfor. Begge variabler er blevet standardiseret, men dette påvirker ikke formen på mønsteret af prikker.
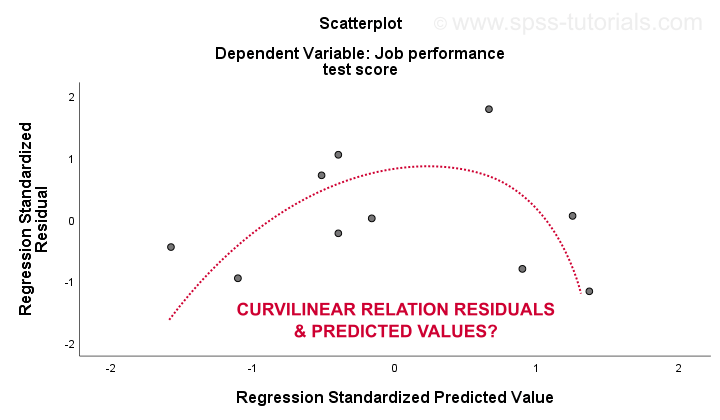
ærligt viser det resterende plot stærk krøllet. Jeg trak manuelt kurven, som jeg synes passer bedst til det samlede mønster. Hvis man antager en krøllet relation, løser det sandsynligvis også heteroscedasticiteten, men tingene bliver alt for tekniske nu.Det grundlæggende punkt er simpelthen, at nogle antagelser ikke holder.De mest almindelige løsninger på disse problemer-fra værste til bedste – er
- ignorerer disse antagelser helt;
- liggende, at regressionsplotterne ikke angiver nogen overtrædelser af modelantagelserne;
- en ikke-lineær transformation – såsom logaritmisk-til den afhængige variabel;
- montering af en krøllet model-som vi giver et skud om et minut.
apa retningslinjer for rapportering Regression
figuren nedenfor er-helt bogstaveligt – en lærebog illustration til rapportering regression i APA-format.

oprettelse af denne nøjagtige tabel fra SPSS-output er en reel smerte i røven. Redigering det går lettere i udmærke sig end i ord, så der kan spare dig en i det mindste nogle problemer.
Alternativt kan du prøve at slippe af sted med at kopiere den (uredigerede) SPSS-udgang og foregive at være uvidende om det nøjagtige APA-format.
ikke-lineært Regressionseksperiment
vores stikprøvestørrelse er for lille til virkelig at passe til noget ud over en lineær model. Men det gjorde vi alligevel-bare nysgerrighed. Den nemmeste mulighed i SPSS er under analyse  Regression
Regression  Kurvestimering.Vi vil ikke diskutere dialogerne, men vi indsatte syntaksen nedenfor.
Kurvestimering.Vi vil ikke diskutere dialogerne, men vi indsatte syntaksen nedenfor.
SPSS ikke-lineær Regressionssyntaks
TSET NYVAR=INGEN.
CURVEFIT
/variabler=ydelse med ik
/konstant
/MODEL= kvadratisk lineær
/PLOT FIT.
resultater
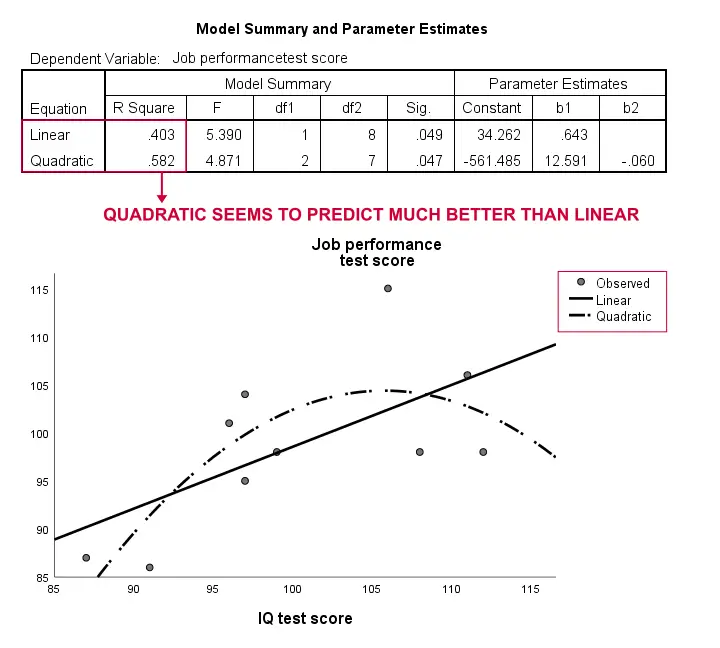
igen er vores prøve alt for lille til at konkludere noget alvorligt. Resultaterne antyder dog lidt, at en krøllet model passer til vores data meget bedre end den lineære. Vi vil ikke udforske dette yderligere, men vi ønskede at nævne det; vi føler, at krøllede modeller rutinemæssigt overses af samfundsvidenskabere.
tak for læsning!




