SPSS Simple Linear Regression Tutorial
- Create Scatterplot with Fit Line
- SPSS Linear Regression Dialogs
- interpretace SPSS regresní výstup
- vyhodnocení regresních předpokladů
- pokyny APA pro vykazování regrese
Výzkumná otázka a Data
společnost X měla 10 zaměstnanců Test výkonu práce. Výsledná data-jejichž část je uvedena níže-jsou v jednoduché lineární regresi.sav.
hlavní věc, kterou společnost X chce zjistit, jeudoes IQ predict job performance? A-pokud ano-jak?Na tyto otázky odpovíme jednoduchou lineární regresní analýzou v SPSS.
Vytvořte Scatterplot s Fit Line
skvělým výchozím bodem pro naši analýzu je scatterplot. To nám řekne, zda skóre IQ a výkonu a jejich vztah-pokud existují – mají vůbec smysl. Vytvoříme náš graf z grafů  starší dialogy
starší dialogy  Scatter / Dot a poté budeme sledovat níže uvedené snímky obrazovky.
Scatter / Dot a poté budeme sledovat níže uvedené snímky obrazovky.
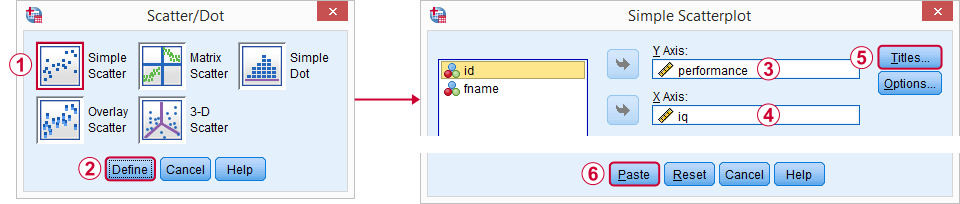
 osobně se mi líbí hodit
osobně se mi líbí hodit
- název, který říká, na co se moje publikum v podstatě dívá, a
- podtitul, který říká, kteří respondenti nebo pozorování jsou zobrazeni a kolik.
procházením dialogů došlo k syntaxi níže. Tak to projdeme.
SPSS Scatterplot se syntaxí titulů
graf
/SCATTERPLOT (BIVAR)=iq s výkonem
/ MISSING=LISTWISE
/ TITLE= ‚Scatterplot Performance with IQ‘
/ subtitle ‚All Respondents | N = 10‘.
výsledek
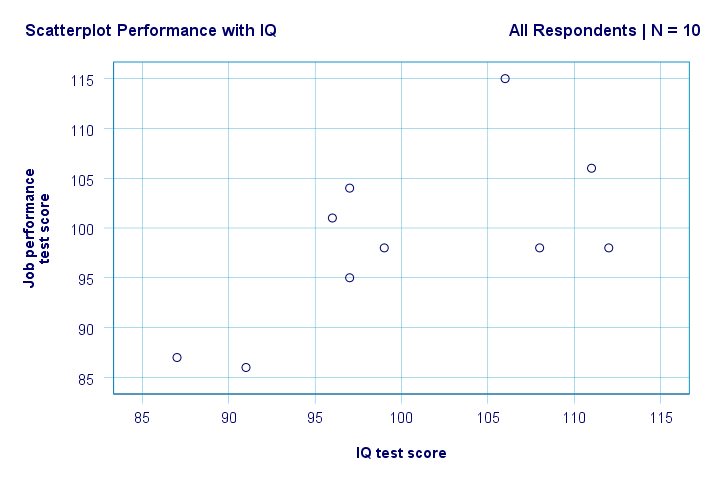
vpravo. Takže za prvé, v našem scatterplot nevidíme nic divného. Zdá se, že existuje mírná korelace mezi IQ a výkonem: v průměru se zdá, že respondenti s vyšším skóre IQ mají lepší výkon. Tento vztah vypadá zhruba lineárně.
pojďme nyní přidat regresní přímku do našeho scatterplot. Klepnutím pravým tlačítkem myši a výběrem možnosti Upravit obsah  v samostatném okně se otevře okno Editoru grafů. Zde jednoduše klikneme na ikonu „přidat řádek přizpůsobení celkem“, jak je uvedeno níže.
v samostatném okně se otevře okno Editoru grafů. Zde jednoduše klikneme na ikonu „přidat řádek přizpůsobení celkem“, jak je uvedeno níže.
ve výchozím nastavení SPSS nyní přidává lineární regresní linii do našeho scatterplot. Výsledek je uveden níže.
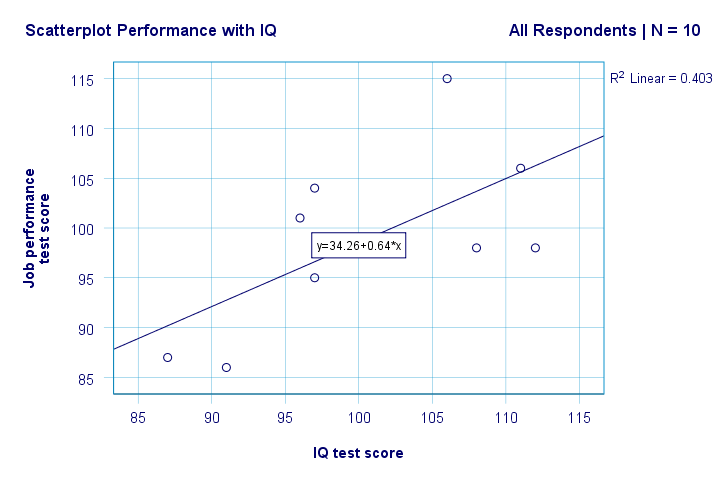
nyní máme několik prvních základních odpovědí na naše výzkumné otázky. R2 = 0.403 znamená, že IQ představuje přibližně 40.3% rozptylu ve skóre výkonu. To znamená, že IQ předpovídá výkon v tomto vzorku poměrně dobře.
ale jak můžeme nejlépe předpovědět pracovní výkon z IQ? No, v našem scatterplot y je výkon (znázorněno na ose y) a x je IQ (znázorněno na ose x). Takže to bude výkon = 34,26 + 0,64 * IQ.So pro uchazeče o zaměstnání s IQ skóre 115, předpovídáme 34.26 + 0.64 * 115 = 107.86 jako jeho / její nejpravděpodobnější budoucí výkonnostní skóre.
správně, takže nám dává základní představu o vztahu mezi IQ a výkonem a prezentuje ji vizuálně. Mnoho informací-statistická významnost a intervaly spolehlivosti-však stále chybí. Pojďme si pro to.
SPSS lineární regresní dialogy
opětovné spuštění naší minimální regresní analýzy z analýzy  regrese
regrese  Lineární nám poskytuje mnohem podrobnější výstup. Níže uvedené screenshoty ukazují, jak budeme postupovat.
Lineární nám poskytuje mnohem podrobnější výstup. Níže uvedené screenshoty ukazují, jak budeme postupovat.
výběr těchto voleb vede k syntaxi níže. Projedeme to.
SPSS jednoduchá lineární regresní syntaxe
REGRESE
/ CHYBÍ LISTWISE
/ STATISTIKA COEFF OUTS CI (95) R ANOVA
/KRITÉRIA=PIN (.05) POUT(.10)
/ NOORIGIN
/ závislý výkon
/ metoda=zadejte iq
/ SCATTERPLOT=(*ZRESID, * ZPRED)
/HISTOGRAM reziduí (ZRESID).
SPSS regresní Výstup I-koeficienty
bohužel nám SPSS dává mnohem více regresního výstupu, než potřebujeme. Většinu z toho můžeme bezpečně ignorovat. Nicméně, tabulka zásadního významu je tabulka koeficientů je uvedeno níže.
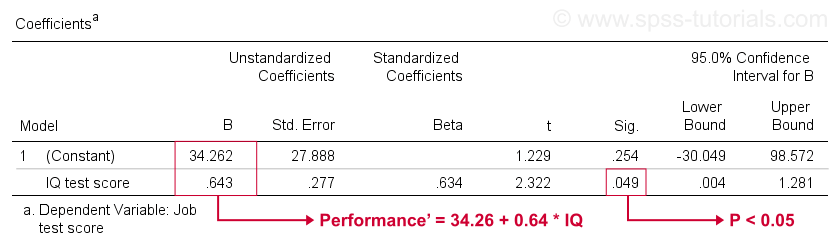
tato tabulka ukazuje B-koeficienty, které jsme již viděli v našem scatterplot. Jak je uvedeno, to znamená lineární regresní rovnici, která nejlépe odhaduje výkon práce z IQ v našem vzorku.
za druhé, nezapomeňte, že obvykle odmítáme nulovou hypotézu, pokud p < 0,05. Koeficient B pro IQ má “ Sig “ nebo p = 0,049. Statisticky se výrazně liší od nuly.
nicméně, jeho 95% interval spolehlivosti-zhruba, pravděpodobný rozsah pro jeho populační hodnotu-je . Takže B pravděpodobně není nula, ale může být velmi blízko nule. Interval spolehlivosti je obrovský – náš odhad pro B není vůbec přesný – a to kvůli minimální velikosti vzorku, na kterém je analýza založena.
SPSS regresní výstup II-souhrn modelu
kromě tabulky koeficientů potřebujeme také souhrnnou tabulku modelu pro hlášení našich výsledků.
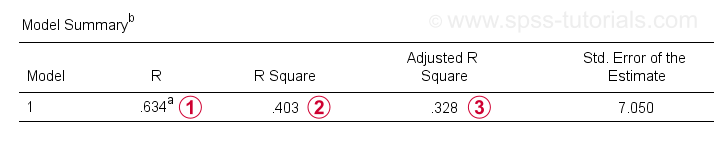
 R je korelace mezi předpovězenými hodnotami regrese a skutečnými hodnotami. Pro jednoduchou regresi se R rovná korelaci mezi prediktorem a závislou proměnnou.
R je korelace mezi předpovězenými hodnotami regrese a skutečnými hodnotami. Pro jednoduchou regresi se R rovná korelaci mezi prediktorem a závislou proměnnou. R čtverec-kvadratická korelace-označuje podíl rozptylu v závislé proměnné, který je účtován prediktorem(s) v našich vzorových datech.
R čtverec-kvadratická korelace-označuje podíl rozptylu v závislé proměnné, který je účtován prediktorem(s) v našich vzorových datech. upravené odhady R-kvadrát R-kvadrát při použití naší (vzorkové) regresní rovnice na celou populaci.
upravené odhady R-kvadrát R-kvadrát při použití naší (vzorkové) regresní rovnice na celou populaci.
upravený R-čtverec poskytuje realističtější odhad prediktivní přesnosti než jednoduše R-čtverec. V našem příkladu je velký rozdíl mezi nimi-obecně označovaný jako smrštění-způsoben naší velmi minimální velikostí vzorku pouze N = 10.
v každém případě je to špatná zpráva pro společnost X: IQ ve skutečnosti nepředpovídá výkon práce tak pěkně.
vyhodnocení regresních předpokladů
hlavní předpoklady regrese jsou
- nezávislá pozorování;
- normalita: chyby musí následovat normální rozdělení v populaci;
- Linearita: vztah mezi každým prediktorem a závislou proměnnou je lineární;
- Homoscedasticita: chyby musí mít konstantní rozptyl nad všemi úrovněmi předpokládané hodnoty.
1. Pokud každý případ (řádek buněk v datovém zobrazení) v SPSS představuje samostatnou osobu, obvykle předpokládáme, že se jedná o „nezávislá pozorování“. Dále jsou předpoklady 2-4 nejlépe vyhodnoceny kontrolou regresních grafů v našem výstupu.
2. Pokud platí normálnost, pak by naše regresní zbytky měly být (zhruba) normálně rozloženy. Histogram níže neukazuje jasný odklon od normality.
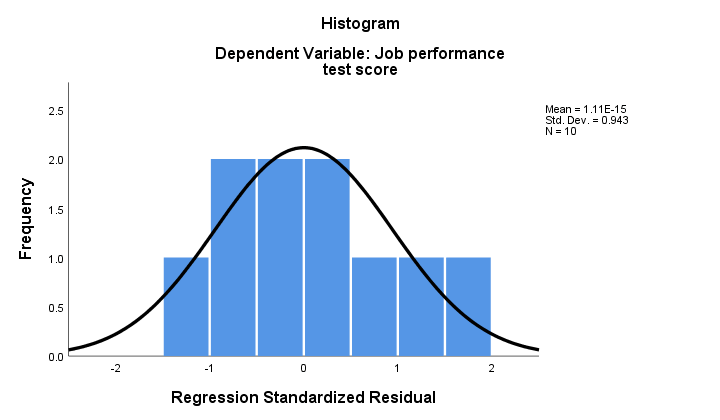
regresní procedura může přidat tyto zbytky jako novou proměnnou do vašich dat. Tímto způsobem byste na nich mohli spustit Kolmogorov-Smirnovův test normality. Pro malý vzorek, který je po ruce, však tento test nebude mít téměř žádnou statistickou sílu. Tak to přeskočme.
3. linearita a 4. homoscedasticity předpoklady jsou nejlépe hodnoceny ze zbytkového grafu. Jedná se o scatterplot s předpovězenými hodnotami v ose x a zbytky na ose y, jak je uvedeno níže. Obě proměnné byly standardizovány, ale to nemá vliv na tvar vzoru teček.
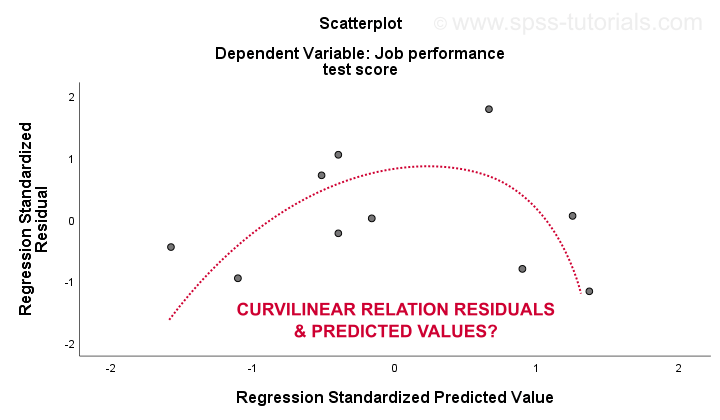
upřímně řečeno, zbytkový graf vykazuje silnou křivost. Ručně jsem nakreslil křivku, o které si myslím, že nejlépe odpovídá celkovému vzoru. Za předpokladu, že křivočarý vztah pravděpodobně vyřeší heteroscedasticitu, ale věci se nyní stávají příliš technickými.Základním bodem je prostě to, že některé předpoklady nedrží.Nejběžnější řešení těchto problémů – od nejhoršího k nejlepšímu-jsou
- ignorování těchto předpokladů úplně;
- lhaní, že regresní grafy nenaznačují žádné porušení modelových předpokladů;
- nelineární transformace-jako je logaritmická-na závislou proměnnou;
- montáž křivočarého modelu-který dáme šanci za minutu .
pokyny APA pro vykazování regrese
níže uvedený obrázek je-doslova-učebnicovou ilustrací pro vykazování regrese ve formátu APA.

vytvoření této přesné tabulky z výstupu SPSS je skutečná bolest v zadku. Editace je v aplikaci Excel snazší než v aplikaci WORD, takže vám může ušetřit alespoň nějaké potíže.
případně se pokuste dostat pryč s kopírováním (neupraveného) výstupu SPSS a předstírejte, že nevíte o přesném formátu APA.
nelineární regresní Experiment
naše velikost vzorku je příliš malá na to, aby se opravdu hodila k čemukoli mimo lineární model. Ale stejně jsme to udělali-jen zvědavost. Nejjednodušší možností v SPSS je analýza  regrese
regrese  odhad křivky.Nebudeme diskutovat dialogy, ale vložili jsme syntaxi níže.
odhad křivky.Nebudeme diskutovat dialogy, ale vložili jsme syntaxi níže.
SPSS nelineární regresní syntaxe
TSET NEWVAR=NONE.
CURVEFIT
/ proměnné=výkon s iq
/ konstanta
/ MODEL= kvadratický lineární
/PLOT FIT.
výsledky
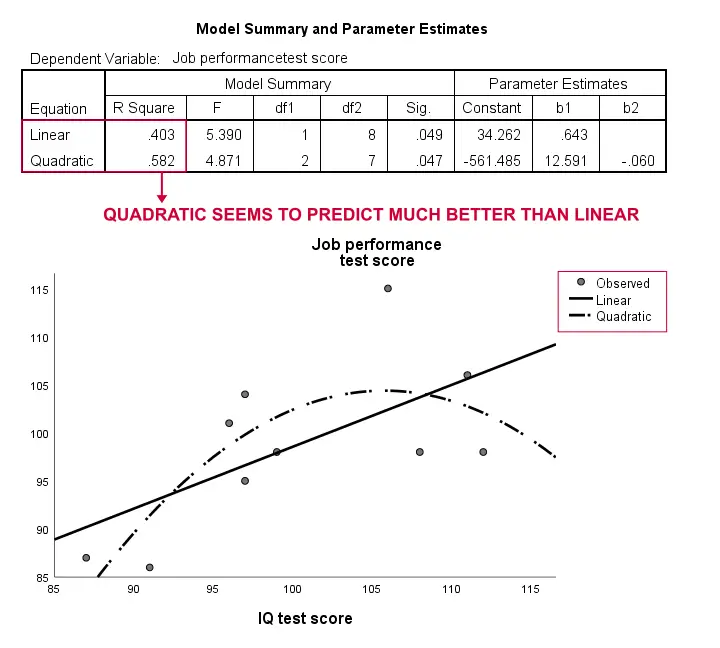
náš vzorek je opět příliš malý na to, aby mohl uzavřít něco vážného. Výsledky však naznačují, že křivočarý model odpovídá našim datům mnohem lépe než lineární. Nebudeme to dále zkoumat, ale chtěli jsme to zmínit; máme pocit, že zakřivené modely jsou sociálními vědci běžně přehlíženy.
Díky za přečtení!




