Come trovare derivati di alto ordine
Trovare un secondo, terzo, quarto o derivato superiore è incredibilmente semplice. La derivata seconda di una funzione è solo la derivata della sua derivata prima. Il terzo derivato è il derivato del secondo derivato, il quarto derivato è il derivato del terzo e così via.
Ad esempio, ecco una funzione e le sue derivate prima, seconda, terza e successiva. In questo esempio, tutte le derivate sono ottenute dalla regola di potenza:
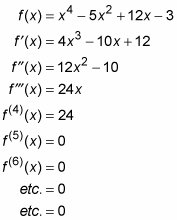
Tutte le funzioni polinomiali come questa alla fine vanno a zero quando si differenziano ripetutamente. D’altra parte, funzioni razionali come
ottieni messier e messier mentre prendi derivati sempre più alti. E i derivati superiori di seno e coseno sono ciclici. Ad esempio,
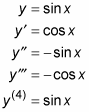
Il ciclo si ripete indefinitamente con ogni multiplo di quattro.
Una prima derivata ti dice quanto velocemente una funzione sta cambiando – quanto velocemente sta andando su o giù-questa è la sua pendenza. Una derivata seconda ti dice quanto velocemente la derivata prima sta cambiando-o, in altre parole, quanto velocemente sta cambiando la pendenza. Una terza derivata ti dice quanto velocemente sta cambiando la seconda derivata, che ti dice quanto velocemente sta cambiando la velocità di cambiamento della pendenza.
Se ti stai perdendo un po ‘ qui, non preoccuparti. Diventa sempre più difficile ottenere una maniglia su ciò che i derivati superiori ti dicono mentre superi la derivata seconda, perché inizi a entrare in un tasso di variazione di un tasso di variazione di un tasso di cambiamento, e così via.




